How do I find the cross product of #<-13, 4># and #<-56, 0>#?
1 Answer
You have two options to evaluate the cross product:
1) the cross product of two vectors
2) evaluate the determinant:
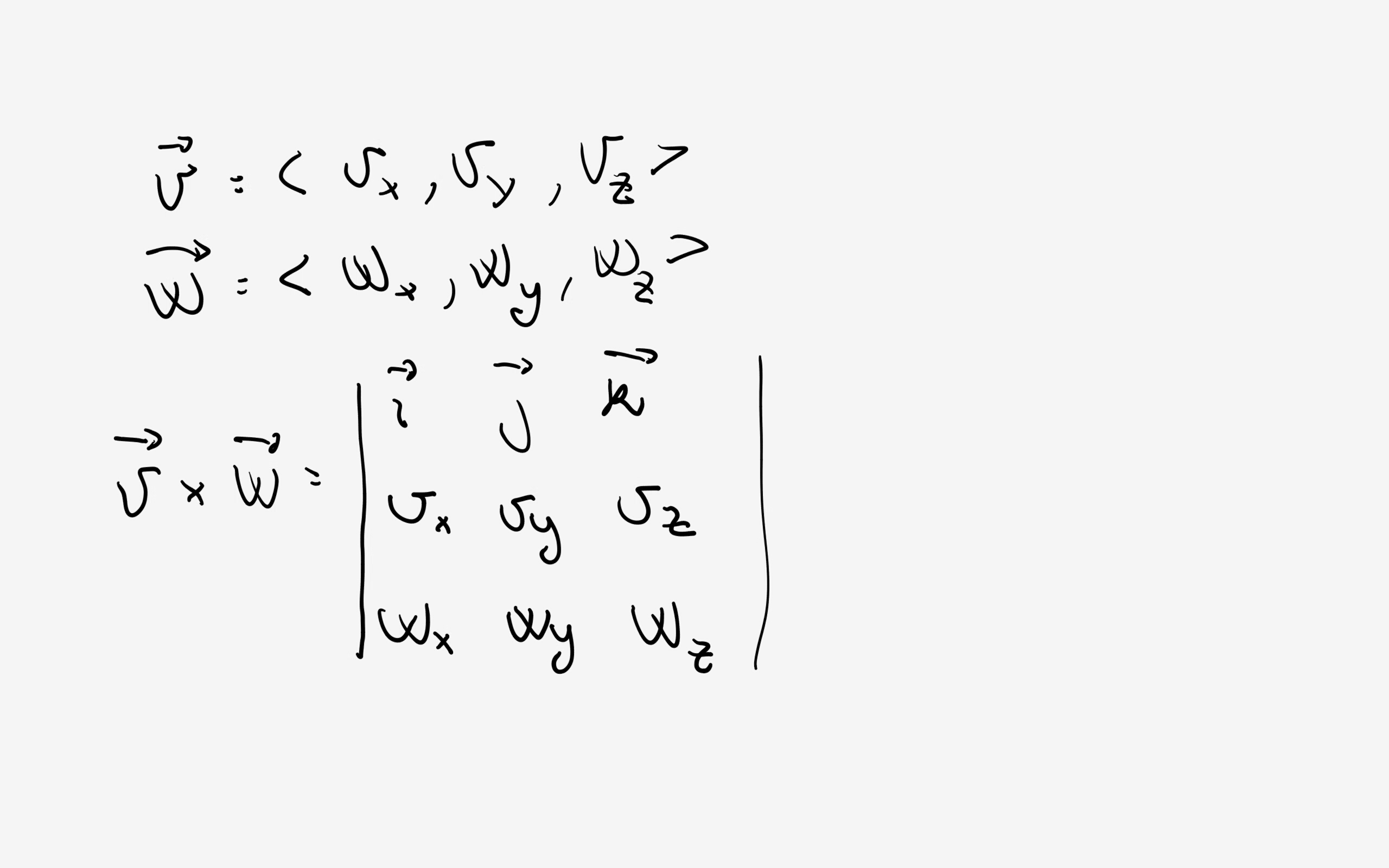
In your case I would use the second option and use the first to check the result. So:
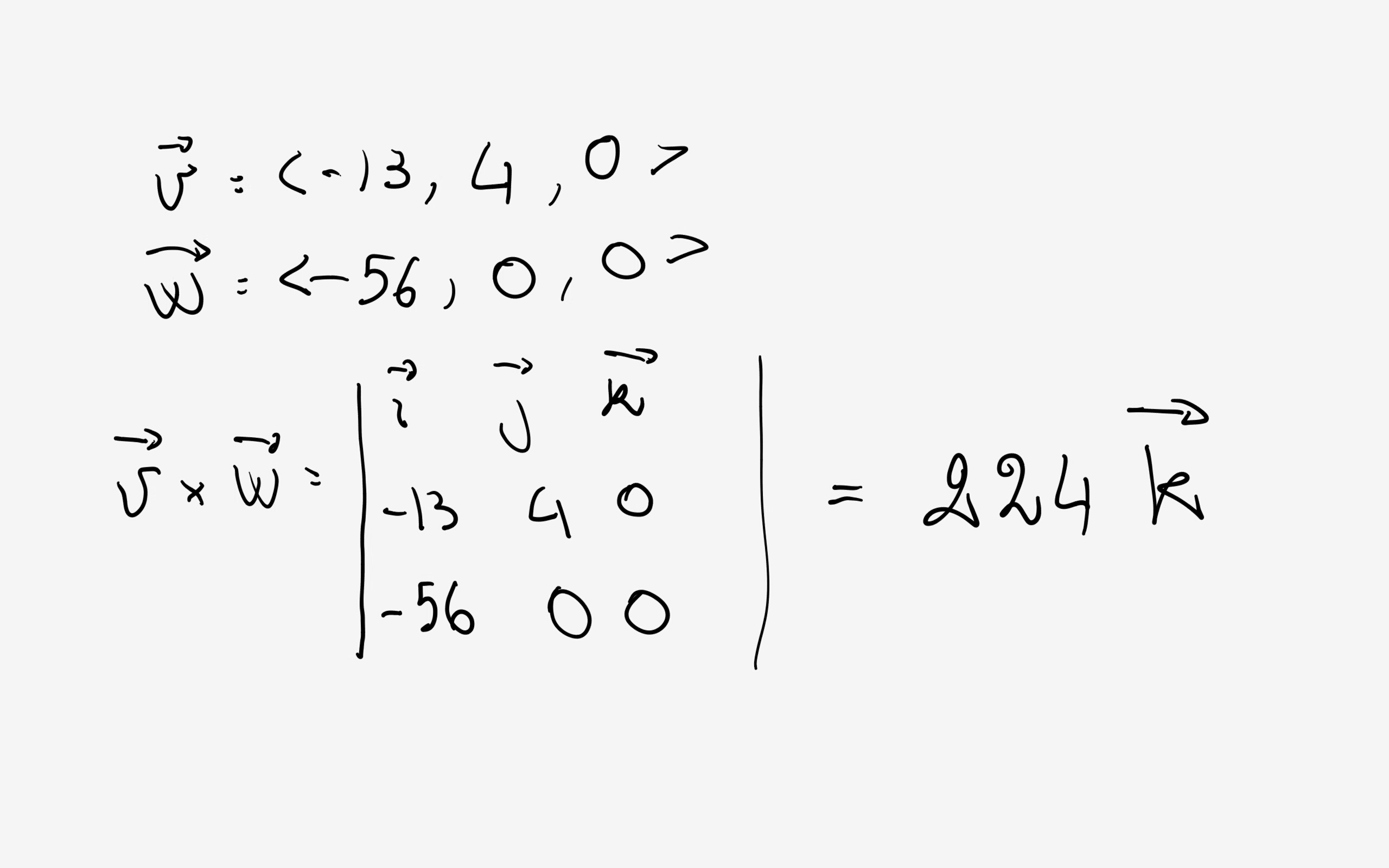
So basically, the result is a vector in the positive
Using the first approach you get the same result considering:
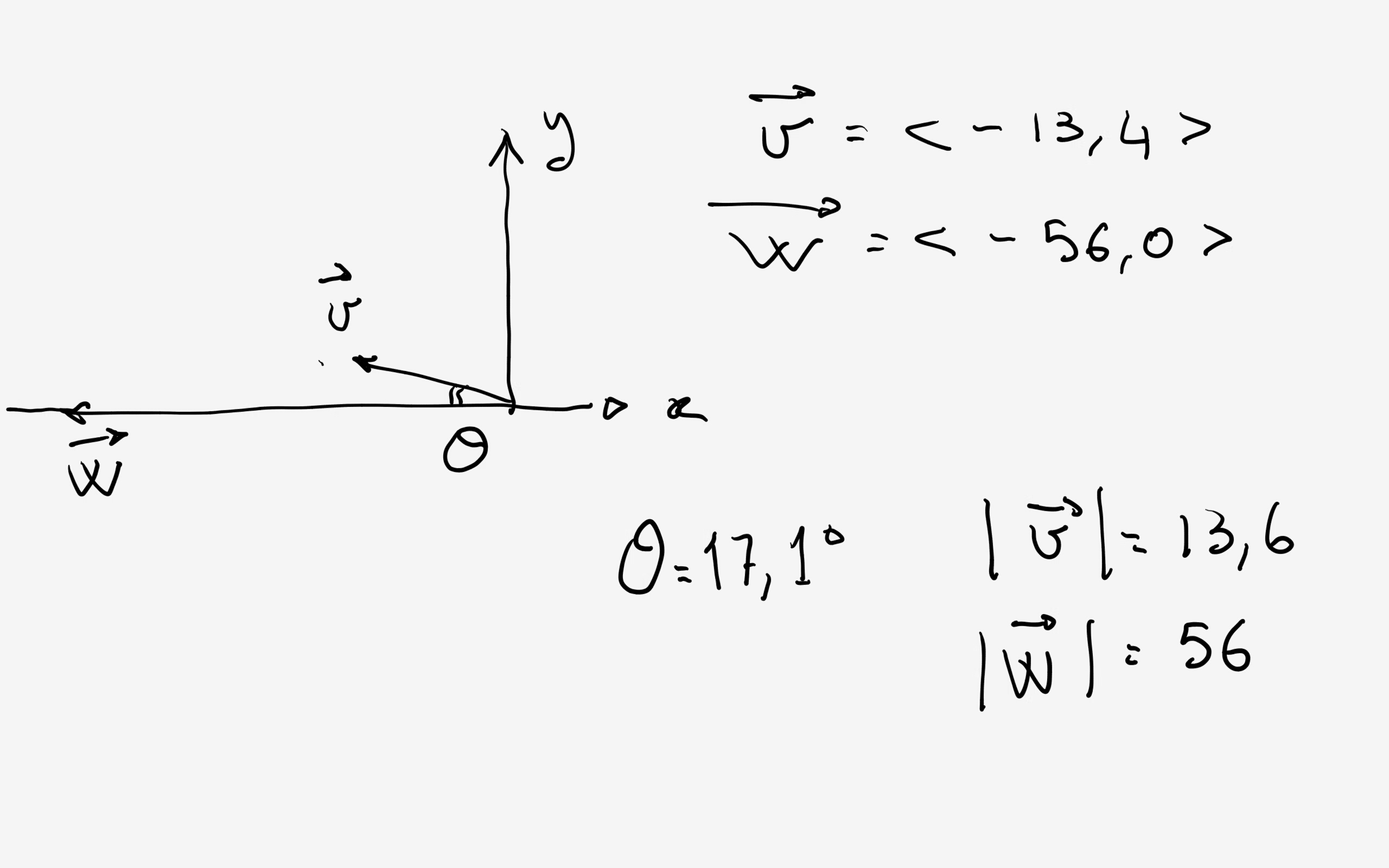
Try to evaluate the modulus (using

