What is the dot product of two vectors?
1 Answer
The dot product of two vectors is a quite interesting operation because it gives, as a result, a...SCALAR (a number without vectorial properties)!
As a definition you have:
Given two vectors
i.e. is equal to the product of the modules of the two vectors times de cosine of the angle between them.
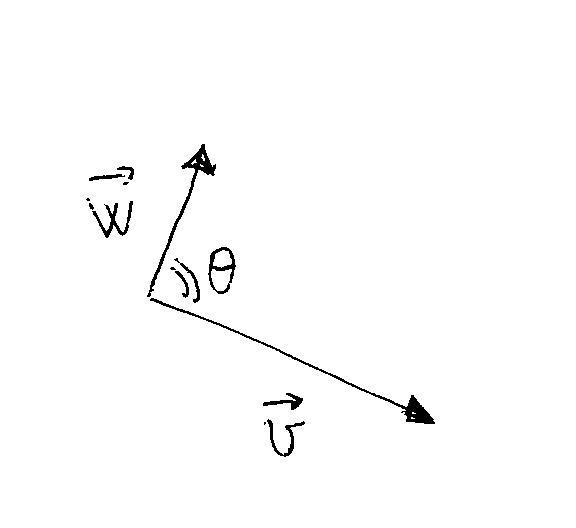
For example:
if
Another way of calculating the dot product is to use the coordinates of the vectors:
If you have:
(where
you can write:
For example:
if:
This operation has important practical applications. For example in Physics the dot product of Force (a vector) and displacement (a vector) gives as a result a number without vectorial characteristics, called, Work.

