Question

What is the cross product of two vectors?

Answer 1

The cross product is used primarily for 3D vectors. It is used to compute the normal (orthogonal) between the 2 vectors if you are using the right-hand coordinate system; if you have a left-hand coordinate system, the normal will be pointing the opposite direction. Unlike the dot product which produces a scalar; the cross product gives a vector.

The cross product is not commutative, so `vec u xx vec v!=vec v xx vec u`. If we are given 2 vectors: `vec u={u_1, u_2, u_3}` and `vec v={v_1, v_2, v_3}`, then the formula is:

`vec u xx vec v={u_2*v_3-u_3*v_2, u_3*v_1-u_1*v_3, u_1*v_2-u_2*v_1}`

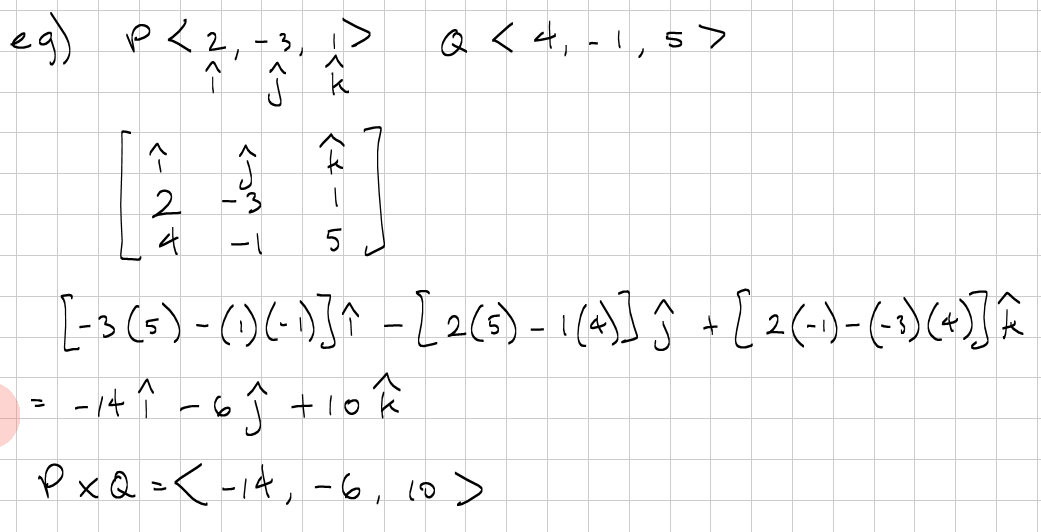
If you have learnt calculating determinants, you will notice that the formula looks a lot like cofactor expansion of the first row; only you don't add up the terms, the terms become the components of the normal. This is one way to remember how to generate the formula for cross product. This is why the middle component is negated in the example.