How do I graph #(x+2)^2/9+(y-1)^2/16=1# algebraically?
1 Answer
You have written about the graph of an ellipse. Since there is addition/subtraction happening with the x- and y-variables, you know that the shape is not centered at the origin.
Solve x + 2 = 0.
x = -2 means "left 2 units"
Solve y - 1 = 0.
y = 1 means "up 1 unit"
Therefore, the center of the figure is (-2,1).
A circle has the same radius in all directions, right? Well, and ellipse has both an x- and a y-radius, determined by the denominators of the expressions involving x- and y-.
Underneath the x term is 9. Take the square root, and call it 3.
Underneath the y term is 16. Take the square root, and call it 4.
Move 3 units right and left from center, and 4 units up and down from center. These are the endpoints of your different "diameters".
See the graph on my TI-nspire below: 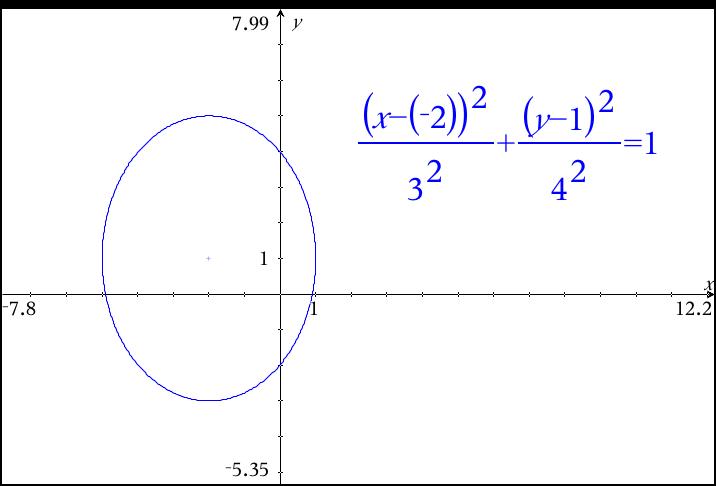
What do you notice about the display of the equation? What is different from your equation?

