How do use the binomial theorem to calculate #""^8C_5#?
3 Answers
Explanation:
so
Explanation:
#"using the definition of "^nC_r#
#•color(white)(x)^nC_r=(n!)/(r!(n-r)!)#
#"where "n! =n(n-1)(n-2)(n-3)......xx3xx2xx1#
#rArr^8C_5#
#=(8!)/(5!3!#
#=(8xx7xx6xxcancel(5xx4xx3))/(cancel(5!)xx3xx2xx1#
#=(8xx7xx6)/6=56#
Explanation:
This seems a curious question to me, since normally you would use
Applying the Binomial theorem to
#(x+1)^8 = ""^8C_0 x^8 + ""^8C_1 x^7 + ""^8C_2 x^6 + ""^8C_3 x^5 + ""^8C_4 x^4 + ""^8C_5 x^3 + ""^8C_6 x^2 + ""^8C_7 x + ""^8C_8#
Taking the derivative
#8 * 7 * 6 (x+1)^5#
#= f^((3)) (x)#
#= 8 * 7 * 6 * ""^8C_0 x^5 + 7 * 6 * 5 * ""^8C_1 x^4 + 6 * 5 * 4 * ""^8C_2 x^3 + 5 * 4 * 3 * ""^8C_3 x^2 + 4 * 3 * 2 * ""^8C_4 x + 3 * 2 * 1 * ""^8C_5#
So:
#8 * 7 * 6#
#= 8 * 7 * 6 * ((color(blue)(0))+1)^5#
#= f^((3)) (0)#
#= 8 * 7 * 6 * ""^8C_0 (color(blue)(0))^5 + 7 * 6 * 5 * ""^8C_1 (color(blue)(0))^4 + 6 * 5 * 4 * ""^8C_2 (color(blue)(0))^3 + 5 * 4 * 3 * ""^8C_3 (color(blue)(0))^2 + 4 * 3 * 2 * ""^8C_4 (color(blue)(0)) + 3 * 2 * 1 * ""^8C_5#
#= 3 * 2 * 1 * ""^8C_5#
So:
#""^8C_5 = (8 * 7 * 6) / (3 * 2 * 1) = 56#
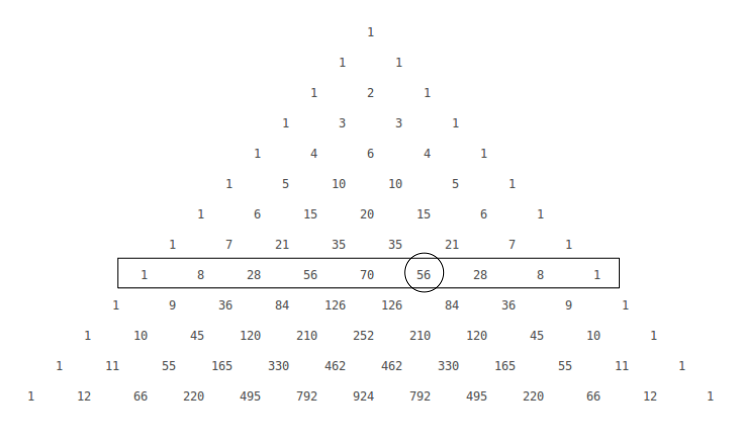
Alternatively, you might recognise that the method of constructing Pascal's triangle relates precisely to the values of the coefficients of
The row of Pascal's triangle starting