Question

How do you add `(2-8i)+(-2+4i)` in trigonometric form?

Answer 1

`(2-8i)+(-2+4i)= 4(cos((3pi)/2)+isin((3pi)/2))`

Explanation:

I will assume that we are allowed to do the addition in rectangular form and then convert the answer into trigonometric form.

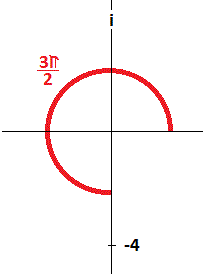
#{: (,,"(",2,-8i,")"), ("+",,"(",-2,+4i,")"), (,,,"-------","-------",), ("=",,"(",0,-4i,")") :}#

The general trigonometric form is
`color(white)("XXX")abs(z)(cos(theta)+isin(theta))`
where
`color(white)("XXX")abs(z)` is the distance from the origin (in the complex plane)
and
`color(white)("XXX")`theta# is the angle of the point (relative to the positive Real axis in the complex plane)