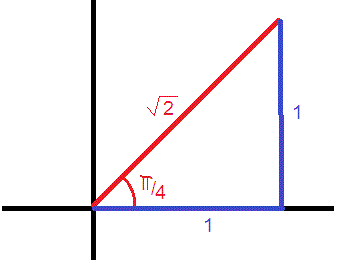
How do you calculate #arctan(1)#?
1 Answer
Nov 28, 2015
Explanation:
If
then
This means that a standard trigonometric triangle will have opposite and adjacent sides of equal length.
(since by definition