How do you calculate #cos^-1 (-0.8)#?
1 Answer
Dec 16, 2015
Explanation:
Since -0.8 is not a value you would find in a trigonometric ratio, which are:
#costheta=-0.8#
#color(white)(xx)theta=cos^-1(-0.8)#
#color(white)(xxx)~~143.13^@#
However, according to the CAST rule, cosine is also negative in the third quadrant, which means there is a second possible answer.
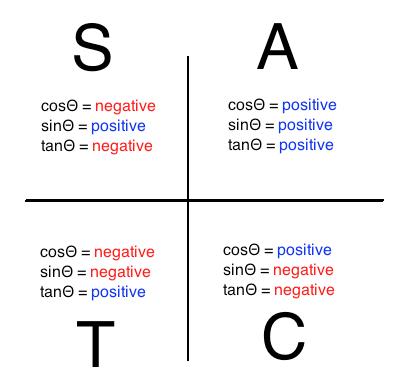
First, find the related acute angle, and add the angle to
Finding the related acute angle
Finding the second possible angle

