Question

How do you calculate `sin x = 0.29`?

Answer 1

You will need to use a trigonometry calculator.

Explanation:

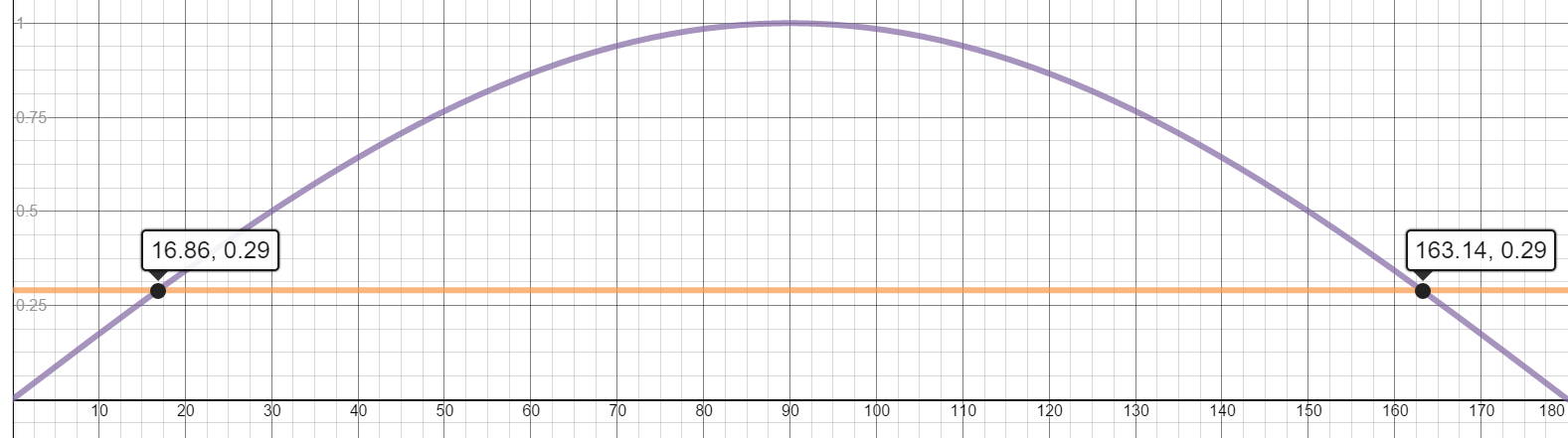
The sine function is positive in the first and second quadrants, so we can conclude that sin x will lie between `0 and 180` degrees. We also know that sine increases to 1 (at `90^o`), then decreases to 0 at `180`.

So, there will be two solutions to this problem. One will occur between `0 and 90` and the other between `90 and 180`.

Using a Trig calculator:

`arcsin(0.29)~~16.858^o`

The other value, due to symmetry, will equal:

`180^o - 16.858^o~~163.142^o`

The graph below shows how the line `y=0.29` intersects the sine graph at the two points `x=16.86^o and 163.14^o`

Hope that helped