How do you change #y - -1/4 = -3(x + 1/4)# into slope intercept form?
3 Answers
Explanation:
This is slope-intercept form:
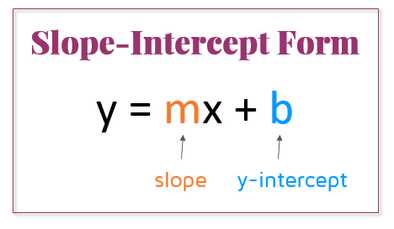
First, simplify:
Now subtract
This now matches slope-intercept form,
Hope this helps!
Explanation:
#"the equation of a line in "color(blue)"slope-intercept form"# is.
#•color(white)(x)y=mx+b#
#"where m is the slope and b the y-intercept"#
#"distribute and rearrange"#
#y+1/4=-3x-3/4#
#"subtract "1/4" from both sides"#
#y=-3x-3/4-1/4#
#y=-3x-1larrcolor(red)"in slope-intercept form"#
Explanation:
Recall that slope intercept form is given by
We can start by distributing the
Next, let's subtract
This equation is now in slope-intercept form.
Hope this helps!


