How do you convert # -2 + 2i# to polar form?
1 Answer
Jul 3, 2016
Explanation:
First we want to draw an Argand diagram.
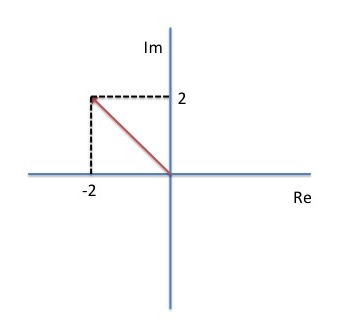
The modulus (or length) of the complex number is simply given by using Pythagoras' theorem to find the hypotenuse, ie
The argument is defined as the angle from the x-axis in the counter-clockwise direction. In this case, the angle we find is in the second quadrant, so we find the 'positive' version and then need to take it away from

