How do you convert #(x-3)^2+(y+1)^2=10# to polar form?

Question

2741 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-09T16:25:35

Polar form of equation is #r=6costheta-2sintheta#

The relation between polar coordinates #(r,theta)# and Cartesian or rectangular coordinates #(x,y)# is given by

#x=rcostheta#, #y=rsintheta# and hence #x^2+y^2=r^2#

Hence we can write #(x-3)^2+(y+1)^2=10# as

#(rcostheta-3)^2+(rsintheta+1)^2=10#

or #r^2cos^2theta-6rcostheta+9+r^2sin^2theta+2rsintheta+1=10#

or #r^2-2r(3costheta-sintheta)=0#

or #r=6costheta-2sintheta#

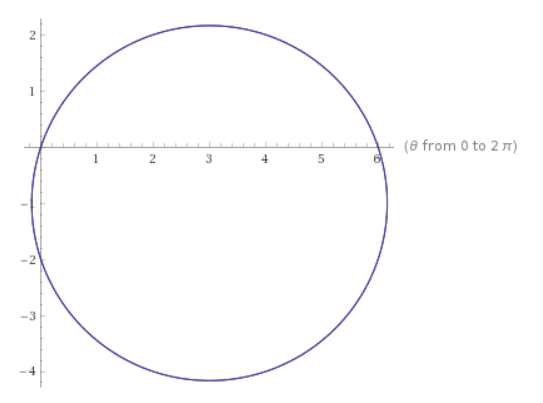
The graph using tool at http://www.wolframalpha.com/ is shown below.

enter image source here