Question

How do you determine whether a linear system has one solution, many solutions, or no solution when given 2x+5y=-16 and 6x+y=20?

Answer 1

A linear system has one solution when the two lines comprising the system intersect once. A linear system has many (infinite) solutions when the two lines are the same (such as `y=x+3` and `2y = 2x+6`). And a linear system has no solution when the lines never intersect (in other words, they're parallel; their slopes are equal).

Explanation:

Here we have the system
`2x+5y = -16`
`6x+y = 20`

To determine the nature of the solutions (whether we have 0, 1, or infinitely many), we put each equation into the form `y = mx+b`, where `m` is the slope and `b` is the y-intercept. To do this, we simply solve for `y`. Let's start with the first equation:

`2x+5y = -16`
`5y = -16-2x`, or equivalently, `5y = -2x-16` (subtracting 2x from both sides)
`y = (-2x-16)/5` (dividing both sides by 5)
`y = -(2x)/5 - 16/5` (putting it into the `y = mx+b` format)

We see that our slope, `m`, is `-2/5` and our y-intercept, `b`, is `-16/5`. Now onto the next equation:

`6x+y = 20`
`y = 20-6x`, or equivalently, `y = -6x+20` (subtracting 6x from both sides)

This time, our slope is `-6` and our y-int. is `20`. Since we have two different slopes (-6 and -2/5), that tells us our linear system has 1 solution. If the slopes were equal, we would have 0 solutions, and if the lines themselves (both slope and y-int.) were the same, we would have infinite solutions. To prove we only have one solution, look at the graph below and see how the lines intersect once.

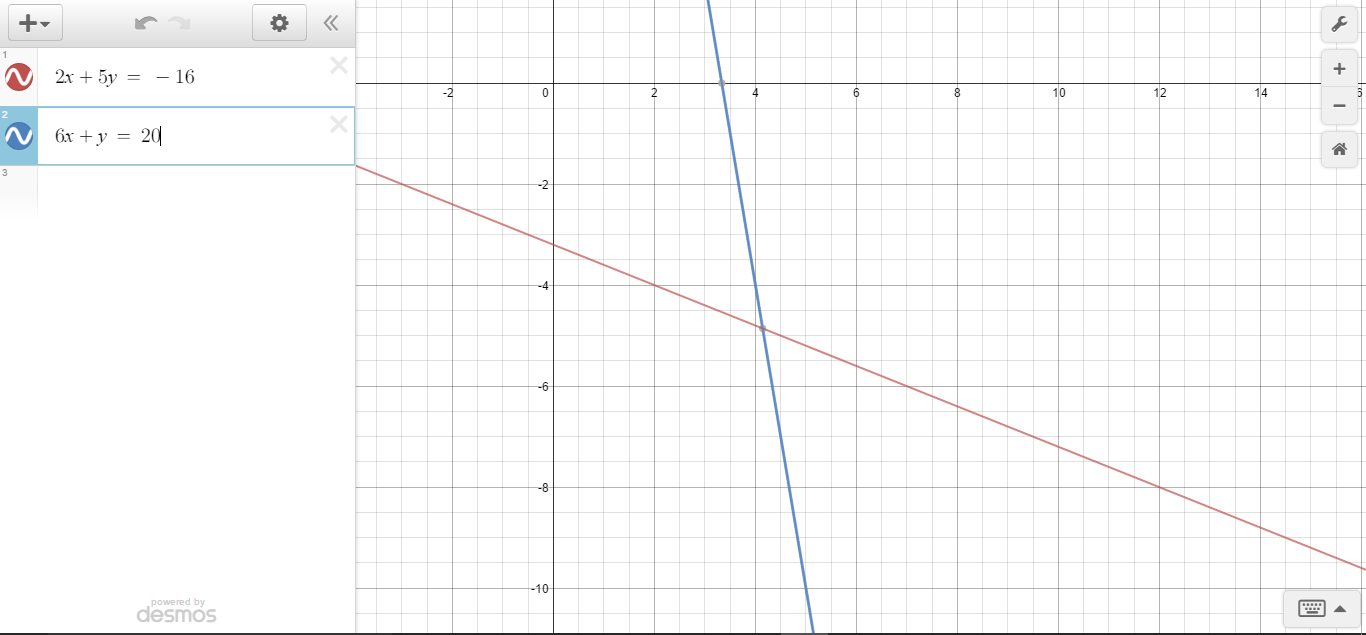
Graph from desmos.com/calculator.