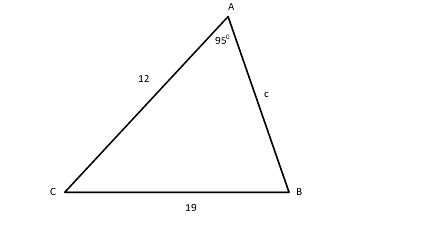
How do you determine whether #triangle ABC# has no, one, or two solutions given #A=95^circ, a=19, b=12#?

Question

3454 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-10T09:04:49

one soltion only

#B=39.0^0, C=46.0^0, c=13.7#

The triangle for this problem is:

NTS

enter image source here

The Sine rule

#a/(sinA)=b/(sinB)=c/(sinC)#

may be used ot find either a side OR an angle if one side and an opposite angle are know.

In this case we need to find an angle first

#19/(sin95)=12/(sinB)=c/(sinC)#

we have to find #sinB# first

#19/(sin95)=12/(sinB)#

#=>sin95/19=sinB/12#

ie

#sinB=(12xxsin95)/19#

#sinB=0.6291755988#

#=>B=38.98932587^0#

#C=180-(95+38.98932587)#

#C=46.01067413^0#

to find the missing side

#c/sinC=19/sin95#

#c=(19xxsinC)/sin95#

#c=13.72213169

so the solution is , all given to 1dp

#B=39.0^0, C=46.0^0, c=13.7#

with the sine rule there is always the possibility of a second set of solutions for the triangle--the AMBIGUOUS case.

to check we take the first angle found

#B=39.9#

subtract from #180^0, because sin(180-x)=sinx#

#B'=180-39.9=140.1#

add this to A

#=95+140.1>180, :. #no second solution