#" "#
Let #color(red)(Z_1 = r_1(Cos theta_1 + i*sin theta_1)#
Let #color(red)(Z_2 = r_2(Cos theta_2 + i*sin theta_2)#
#color(blue)((Z_1/Z_2) = (r_1/r_2)[cos (theta_1 - theta_2)+i*sin(theta_1 - theta_2)]#
Consider the problem given:
#color(green)(Z_1 = (-4-9i)# and
#color(green)(Z_2 = (6-2i)#
In complex numbers,
we know that #i=sqrt(-1) and i^2=(-1)#
#Z_1/Z_2=(-4-9i)/(6-2i)#
Multiply and divide by the Conjugate of the denominator to simplify.
#Z_1/Z_2=(-4-9i)/(6-2i)*color(red)((6+2i)/(6+2i)#
#rArr [-24-8i-54i-18(i^2)]/(36-(2i)^2#
#rArr [-24-62i+18]/[(36+4)]#
#rArr (-62i-6)/40#
#rArr (2(-31i-3))/(2*20)#
#rArr (cancel 2(-31i-3))/(cancel 2*20)#
#rArr (-3-31i)/20#
#color(blue)( :. Z_1/Z_2= -(3/20)-(31/20)i#
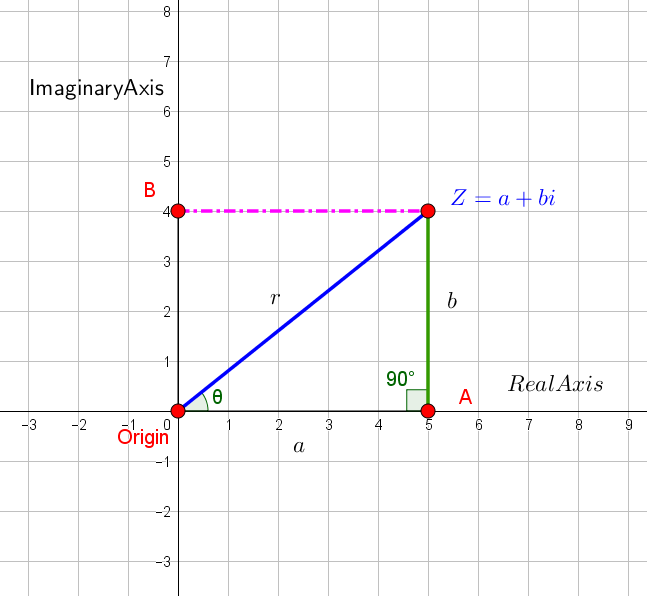
Express #color(blue)(r# in terms of #color(blue)(a and b#.
Using Pythagoras Theorem,
#r^2=(a^2+b^2)#
#r=sqrt(a^2+b^2)#
#|z|=a+bi#
#|z| = sqrt(a^2+b^2#
#sin(theta)=b/r#
#rArr color(red)( b=r*sin(theta)#
#cos(theta) = a/r#
#rArr color(red)( a=r*sin(theta)#
We already have
#color(blue)( Z_1/Z_2= -(3/20)-(31/20)i#
#|z|=sqrt((-3/20)^2+(-31/20)^2#
Simplifying you get
#rArr sqrt(970/400#
#rArr sqrt(970)/20#
To find #color(red)(theta#
#theta = tan^-1[(-31/20)/(-3/(20)]]#
Using the calculator to simplify, you get
#theta ~~ 84.47245985^@#
# :. theta ~~ 84.5^@#
You have to add 180 to the angle when you recognize that the angle lies in the third quadrant.
Hence #theta ~~84.5^@ + 180^@#
#rArr theta ~~ 264^@#
Hence, the final representation of #Z# will be
#color(red)(Z=sqrt(970)/20[cos(264^@)+i*sin(264^@)]#
Hope it helps.


