How do you divide #( 8i+2) / (-i +2)# in trigonometric form?
1 Answer
The key to solve this problem is to know trigonometric form of a complex number.
Explanation:
Tip: this is just a theoretical introductory; you can jump to the text below the image to see the problem solution.
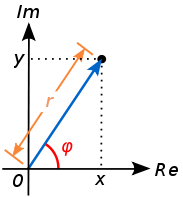
A complex number
- Binomial form:
#z = x + y cdot "i"#
where#a# is the real part and#b# the imaginary part. - Cartesian form:
#z = (x, y)#
just as the binomial form, but written as an ordered pair. - Polar form:
#z = r_phi#
where#r# is the modulus (or absolute value) of the number and#theta# is the argument.
-- The modulus is obtained by:#r = sqrt{x^2+y^2}#
-- The argument is obtained by:#phi= arctan(y/x)# . It must be always between#-pi/2# and#pi/2# - Cartesian form:
#z = r cdot (cos phi+ "i" cdot sin phi)# - Exponential form:
#z = r cdot e^phi#
where#e# is the exponential.
To sum up, there are two ways to represent a complex number:
- Depending on its coordinates,
- Depending on its vectorial magnitudes,
If we want to add and substract complex numbers, we should use cartesian or binomial forms; however, if we want to solve a product or a fraction, we should use polar form, and then transform into the one which interests us.
Let us divide
First of all, we must transform both numbers (numerator and denominator) from binomial to polar form, and then we will transform the result into trigonometric form.
#8 "i" + 2 = 8.2462_1.33# #-"i" + 2 = 2.2361_{-0.46}#
And now, we divide both modulus, and we substract both arguments:
Finally, we transform it into trigonometric form:

