How do you do simplify cos [sec ^-1 (-5)]?
1 Answer
Nov 6, 2015
Explanation:
Finding the value of the Composition:
Lets being to solve the equation by working on the inside. Immediately we can see that
Note: The inverse of cosine (secant) is restricted between
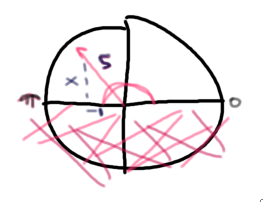
Now cosine is
This is not a special angle so leave the answer as a improper fraction or decimal. Whatever your instructor prefers. :)
