How do you evaluate #arccos(sqrt3/2)# without a calculator?
1 Answer
Dec 27, 2016
Explanation:
If we split an equilateral triangle (in which all interior angles
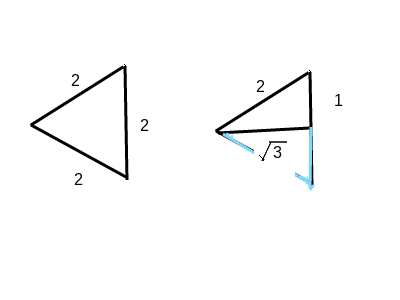
we will get an angle
(Note that there is also the angle
