How do you evaluate #arcsin(1)# without a calculator?
1 Answer
Explanation:
Arcsin is the reverse of the sine function - that is, it looks at a ratio and asks what angle can create that ratio.
Here we have
We can express this sin ratio as
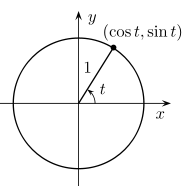
Look at the point where the line segment and circle meet. The line segment is the hypotenuse of a circle and the opposite is a line dropped from that point down on to the x-axis. If we move the point along the circle towards the y-axis, the opposite side gets longer and starts to approach the same length as the hypotenuse. It's at the point where the line segment stretches straight up the y-axis, and consequently the opposite side does as well, that we get the equal length needed. That angle is

