How do you evaluate arctan(-1) using a unit circle?
1 Answer
Apr 21, 2015
Using a unit circle centered at
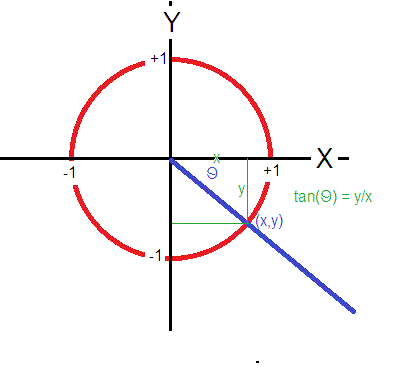
Asking for
for
This will happen when
Within the domain
this only happens at
and
