How do you evaluate #arctan((sqrt (3)) /3)#?
2 Answers
Apr 26, 2016
Explanation:
Note that
Here is a standard trigonometric triangle with this ratio for the tan:
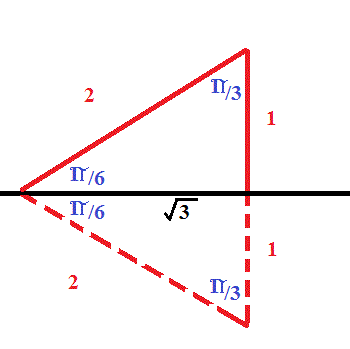
Note that by definition the
Apr 26, 2016
Explanation:
Thanks to Alan for the timely correction, over my seeing
If a is a solution in
Here,
