How do you evaluate #cos^-1[cos(-pi/2)]#?

Question

13200 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-13T04:15:56

#pi/2#

Cosine is an even function, meaning #cos(-x)=cosx#.

So, #cos(-pi/2)=cos(pi/2)=0#

Then, we really want

#cos^-1(0) = x -> cos(x)=0 -> x=pi/2# as the domain of the inverse cosine is #[-1, 1]#.

Answer 2 · 2018-04-13T04:21:53

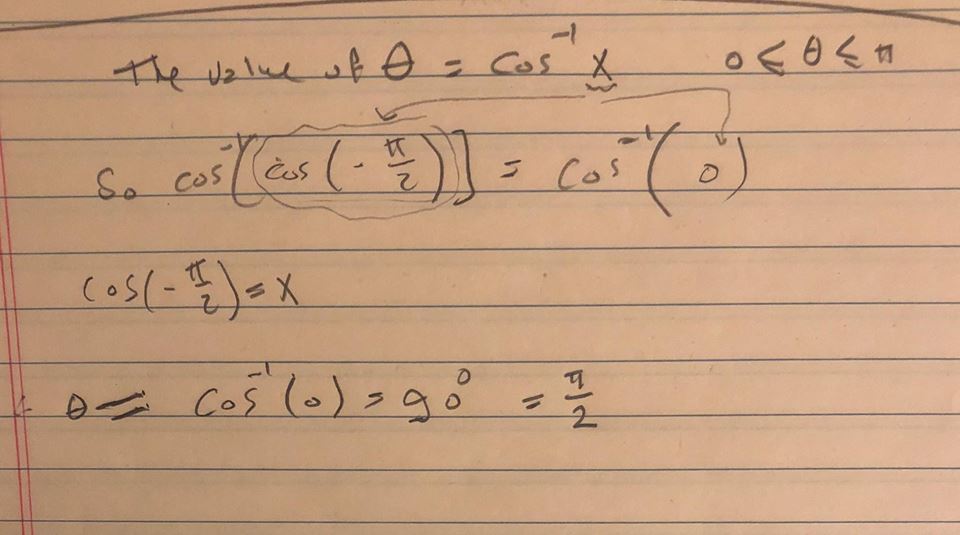
90 or Pi/2

check the attached picture.