How do you evaluate #cos (arcsin (3/5))#?

Question

26797 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-26T06:55:54

#cos(arcsin(3/5)) = 4/5#

The ratio #3/5# should probably be a clue.

Note that #arcsin(x) in [-pi/2, pi/2]# and if #0 < x < 1# then #arcsin(x) in (0, pi/2)#.

So #arcsin(3/5)# is an angle in Q1, which we can consider in a right-angled triangle.

Consider a #3#, #4#, #5# (right) triangle:

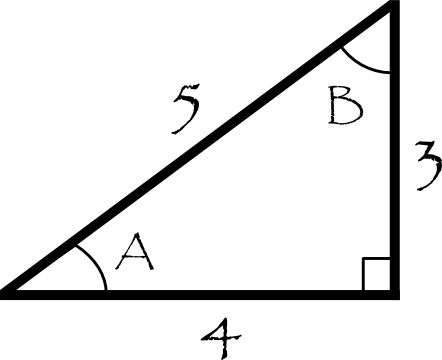
enter image source here

We have:

#sin A = "opposite"/"hypotenuse" = 3/5#

#cos A = "adjacent"/"hypotenuse" = 4/5#

So:

#cos(arcsin(3/5)) = cos(A) = 4/5#

Alternatively, we could note more generally that:

#cos^2 theta + sin^2 theta = 1#

Hence:

#cos theta = +-sqrt(1-sin^2 theta)#

If #theta = arcsin(x)#, then #theta in [-pi/2, pi/2]# and hence #cos theta >= 0# and we find:

#cos(arcsin(x)) = sqrt(1-x^2)#

Answer 2 · 2018-05-27T02:54:14

The inverse sine is multivalued, so

#cos arcsin(3/5) = pm sqrt{1-(3/5)^2} = pm 4/5 #