How do you evaluate #cos(sin^-1((sqrt3/2))# without a calculator?

Question

15815 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-04T19:24:56

#cos(sin^(-1)(sqrt(3)/2)) = 1/2#

Consider an equilateral triangle with sides of length #2#, bisected to form two right angled triangles:

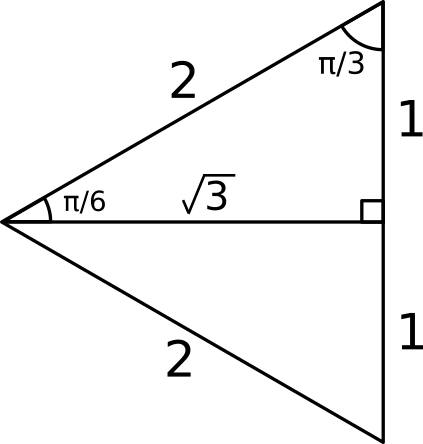
enter image source here

Remembering that #sin = "opposite"/"hypotenuse"#, we can see that:

#sin(pi/3) = sqrt(3)/2#

Since #sqrt(3)/2 > 0# and #pi/3# is in Q1, we can deduce:

#sin^(-1)(sqrt(3)/2) = pi/3#

From the same diagram, remembering #cos = "adjacent"/"hypotenuse"#, we can see that:

#cos(pi/3) = 1/2#

So:

#cos(sin^(-1)(sqrt(3)/2)) = cos(pi/3) = 1/2#

Answer 2 · 2017-02-04T19:30:54

#cos(sin^(-1)(sqrt(3)/2)) = 1/2#

Starting from:

#cos^2 theta + sin^2 theta = 1#

Subtract #sin^2 theta# from both sides to get:

#cos^2 theta = 1 - sin^2 theta#

Take the square root to find:

#cos theta = +-sqrt(1-sin^2 theta)#

If #theta = sin^(-1)(sqrt(3)/2)# then #sin(theta) = sqrt(3)/2# and we find:

#cos theta = +-sqrt(1-(sqrt(3)/2)^2) = +-sqrt(1-3/4) = +-sqrt(1/4) = +-1/2#

Further note that #sqrt(3)/2 > 0#, so #sin^(-1)(sqrt(3)/2)# must be in Q1. Hence #cos theta > 0# and we need to choose the positive square root.

So:

#cos(sin^(-1)(sqrt(3)/2)) = 1/2#