How do you evaluate #sec^-1( 2/ sqrt3)#?
2 Answers
Explanation:
Ask yourself: "secant of what angle gives me
Since
We know that
While secant is also positive in quadrant four, and there are an infinite amount of coterminal angles where secant is
Explanation:
#sec^-1(2/sqrt(3))#
#sectheta=2/sqrt(3)#
#1/costheta=2/sqrt(3)#
#costheta=sqrt(3)/2#
#theta=cos^-1(sqrt(3)/2)#
#theta=30^@#
However, since
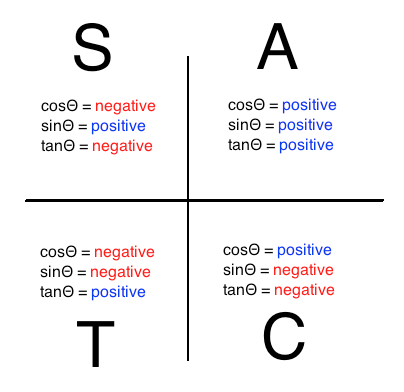
To find the other angle that would also give an answer of
#360^@-30^@#
#=330^@#


