How do you evaluate #tan^-1(sqrt3/3)# without a calculator?

Question

3070 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-09-29T21:23:21

#tan^(-1) (sqrt(3)/3) = pi/6#

Consider a triangle with sides in ratio #1:sqrt(3):2#

This is a right angled triangle since:

#1^2+sqrt(3)^2 = 1+3 = 4 = 2^2#

In fact, it is one half of an equilateral triangle, hence has angles #pi/6#, #pi/3#, #pi/2#...

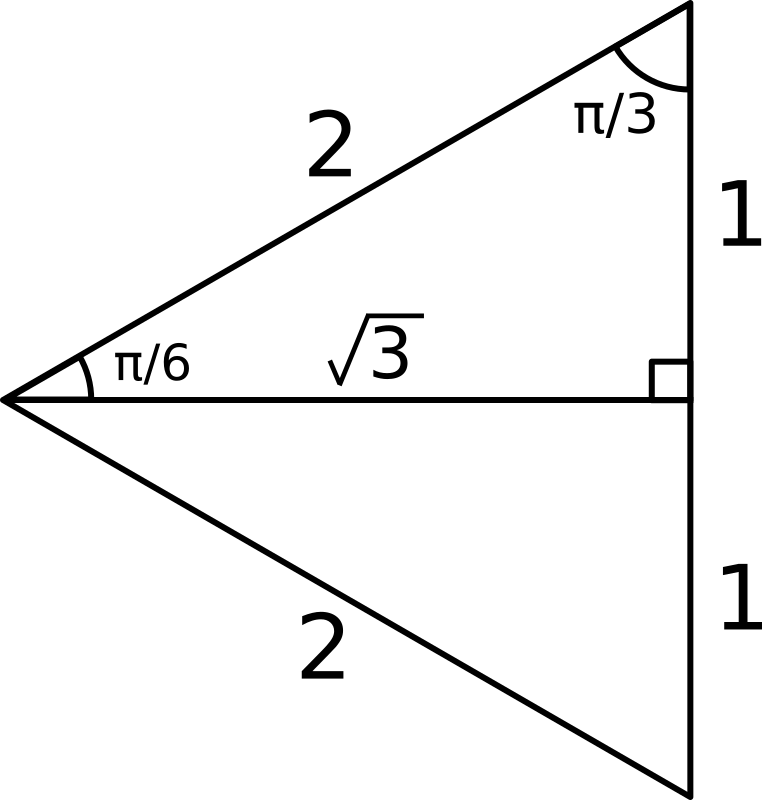
enter image source here

Now #tan(theta) = "opposite"/"adjacent"#

Hence we find:

#tan (pi/6) = 1/sqrt(3) = sqrt(3)/3#

Since #pi/6# radians is in Q1, this is the value of #tan^(-1) (sqrt(3)/3)#