How do you expand (4x – 3y)^4# using Pascal’s Triangle?
1 Answer
The Pascal's Triangle is a number triangle where the numbers in each consecutive row going down from the top are the sum of the two numbers directly above it.
Explanation:
The following diagram shows the Pascal's Triangle.
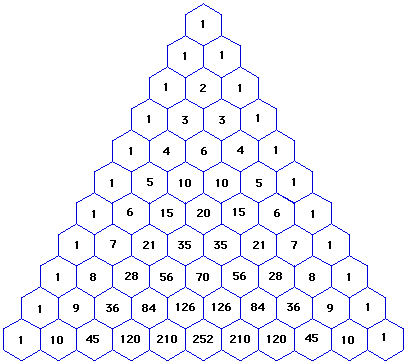
The reason that the triangle relates to the expansion of a binomial is because the coefficients in a given row replace
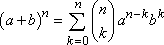
Before expanding your binomial though, we must find the number of terms in the expansion. In a binomial of the form
The numbers in the 5th row of the Pascal's triangle are
Thus, you have your answer. Always make sure to use a test point in your a) original expansion and b) your final answer. I know from experience that errors can very often occur in this process because you will handle big numbers and you will have to calculate a lot. The trick: take your time.
I selected the following test point:
In the original expression, this would give
Calculating in the answer, we get the same thing. Thus, we have the correct answer.
Hopefully this helps!

