Question

How do you expand `(x-3)^5` using Pascal’s Triangle?

Answer 1

See solution below.

Explanation:

Here is Pascal's Triangle:

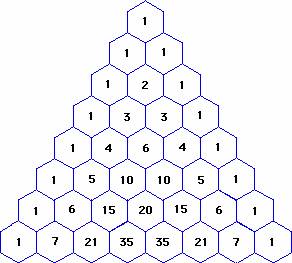
What do you notice?

You should notice that the numbers as you go down are the sum of the numbers to the upper left and upper right of them. You should notice also that the rows always start and end with 1. Also, the sum of each row can be written in the form `2^(n - 1)`, where `n` is the row number.

To expand binomials using the Pascal's Triangle, we must make the exponents on the first term (x) descending and the exponents on the second term (-3) augmenting. We must also multiply the answer to each expression by the numbers in the `n + 1` row of the Pascal's Triangle, in order, in `(x - p)^n`.

The exponent in the expression is 5, and so the expansion will have 6 terms. What are the numbers in the 6th row of the Pascal's Triangle?

Counting down from the row with the single 1, we find that the sixth row is the row with six terms: 1, 5, 10, 10, 5 and 1 respectively.

`(1 xx (x)^5 xx (-3)^0) + (5 xx (x)^4 xx (-3)^1) + (10 xx (x)^3 xx (-3)^2) + (10 xx (x)^2 xx (-3)^3) + (5 xx (x)^1 xx (-3)^4) + (1 xx (x^0) xx (-3)^5)`

`= x^5 - 15x^4 + 90x^3 - 270x^2 + 405x - 243`

So, `(x - 3)^5 = x^5 - 15x^4 + 90x^3 - 270x^2 + 405x - 243`

Practice exercises:

1. Use Pascal's triangle to expand the following.

a) `(2x + 5)^4`

b) `(3x - 2y)^7`

For questions 2 and 3 use the formula `t_(r + 1) = a^(n - r) xx b^r`

1. Find the 10th term of `(2x + y^3)^14`

2. Find the constant term in `(3x^2 + 4)^8`. Note: a constant term is a term that has no variable coefficient (46 is a constant term while 46x is not).