How do you factor by grouping #x^3-12-3x^2+4x#?
2 Answers
Apr 9, 2015
Have a look:
Collect between the 1st and 3rd term and between 2nd and 4th:
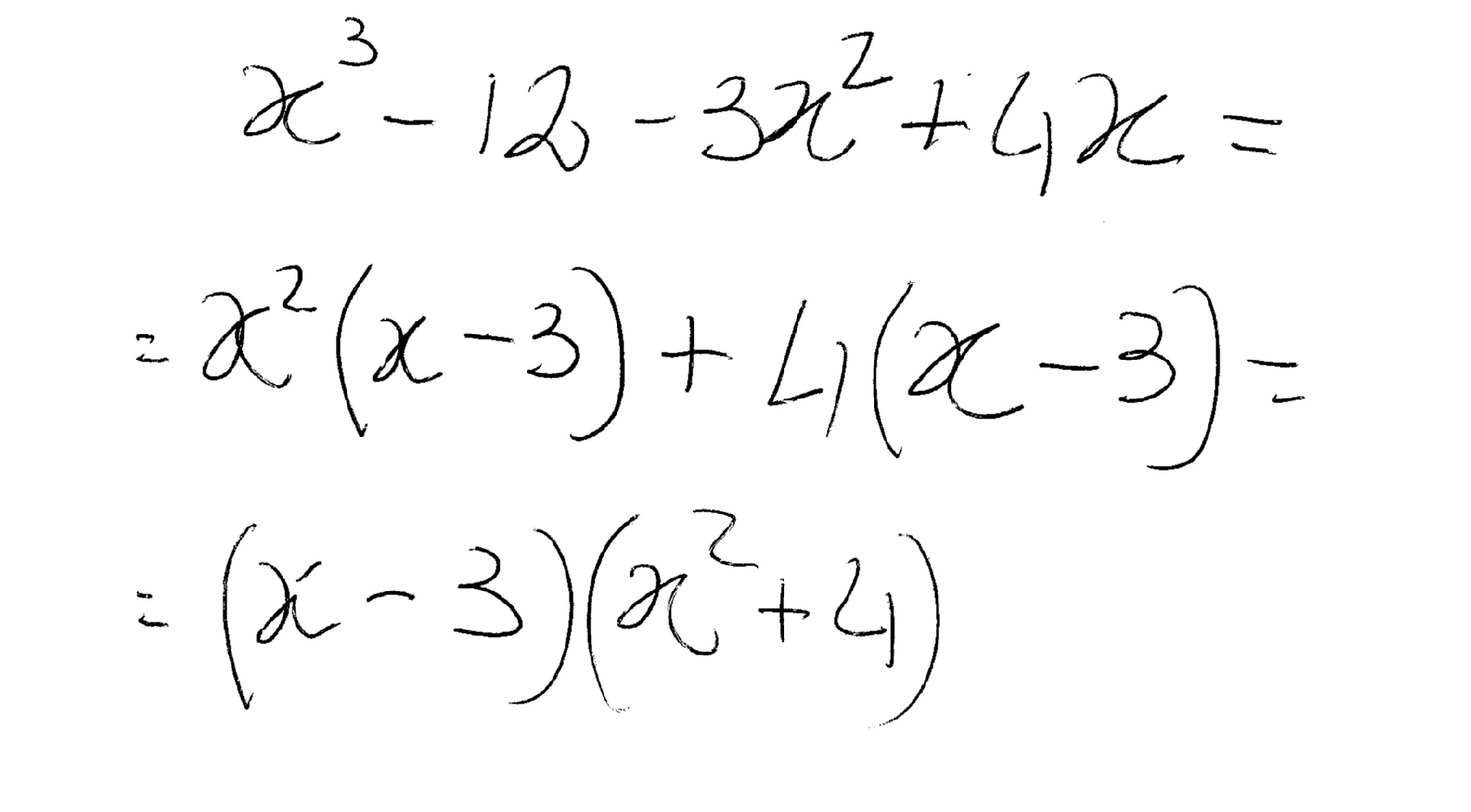
Apr 9, 2015
can be re-grouped as
which can then be factored as
then combining the common factor from each term

