How do you factor x³+x²-x-1?
2 Answers
The complete factorization is
Explanation:
I used synthetic division to solve this. (Do you need further explanation?)
You can factor by grouping to find:
x^3+x^2-x-1 = (x^2-1)(x+1)
Then use the difference of squares identity to find:
(x^2-1)(x+1) = (x-1)(x+1)(x+1) = (x-1)(x+1)^2
Explanation:
First factor by grouping:
x^3+x^2-x-1 = (x^3+x^2)-(x+1) = x^2(x+1)-1(x+1) = (x^2-1)(x+1)
Then notice that
(x^2-1)(x+1) = (x-1)(x+1)(x+1) = (x-1)(x+1)^2
Alternatively, notice that the sum of the coefficients (
Divide
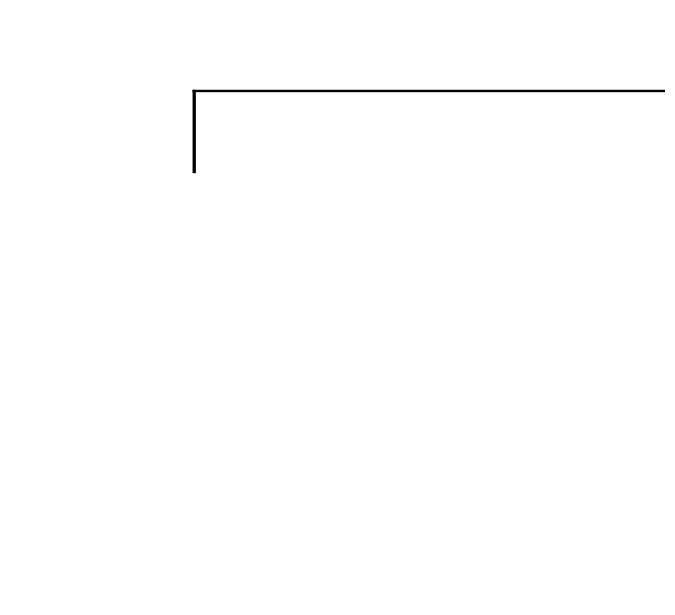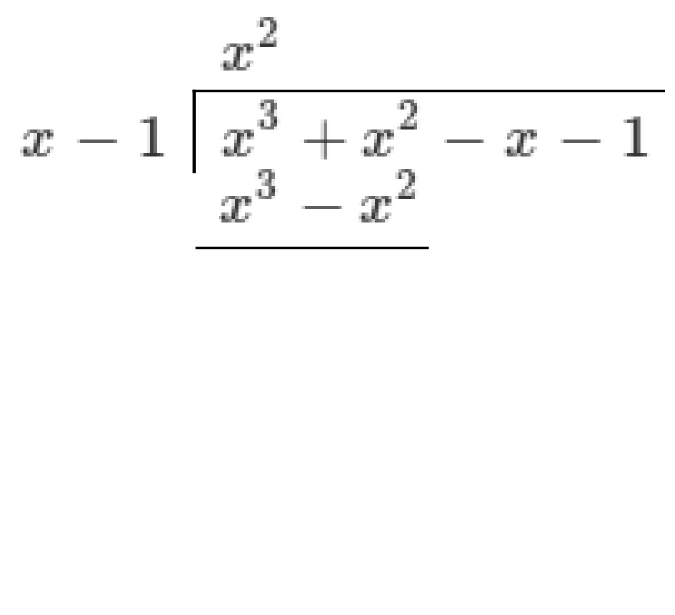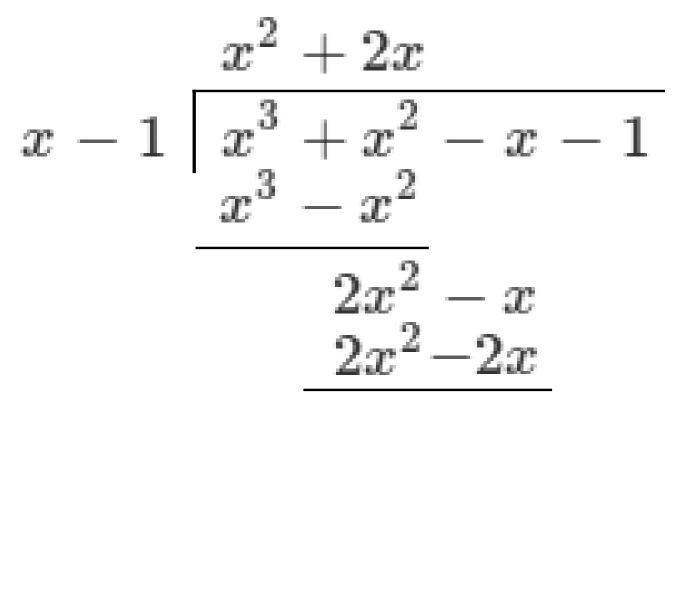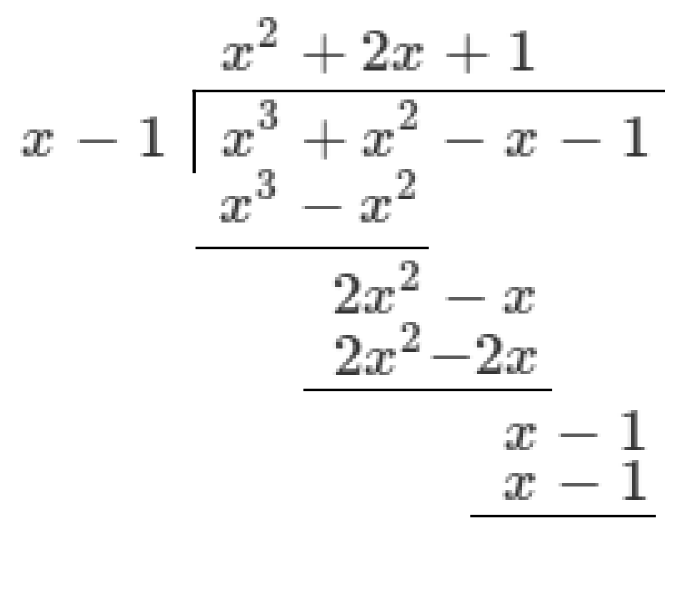
Then recognise that


