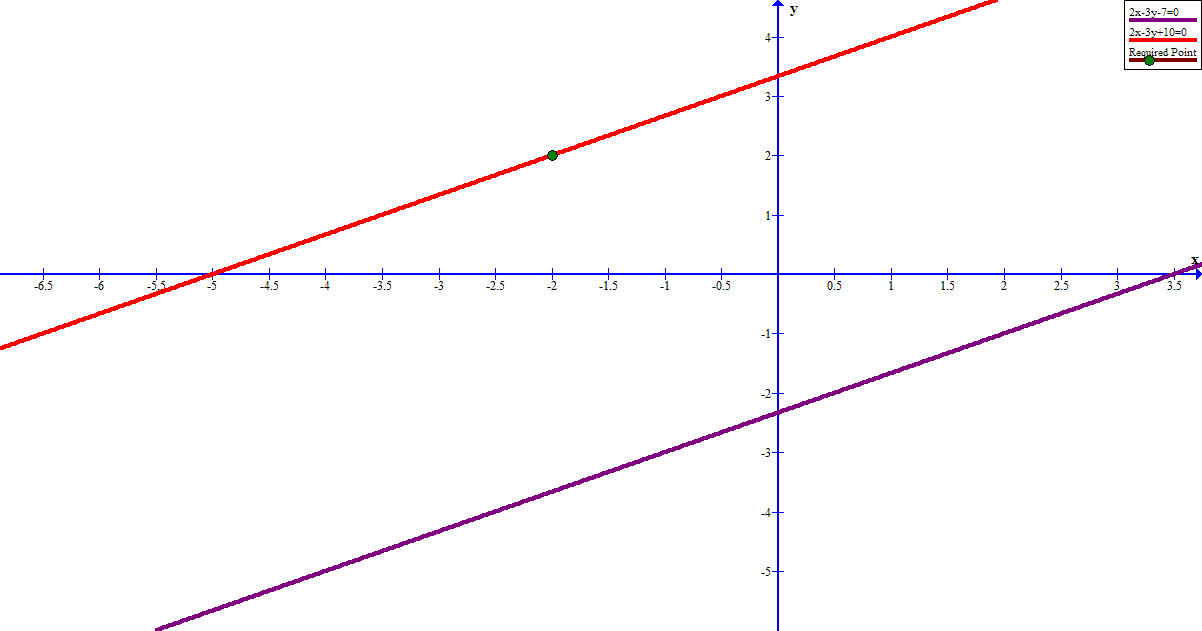
#2x-3y-7=0# and any line parallel to it has a slope of #color(green)(m=2/3)#
#color(white)("XXX")#We know this either because:
#color(white)("XXX")[1]color(white)("XX")#we know #Ax+By+c=0# has a slope of #color(green)(-A/B)#
#color(white)("XXX")#or
#color(white)("XXX")[2]color(white)("XX")# by converting into slope-intercept form: #y=color(green)(m)x+b#
~~~~~~~~~~~~~~~~~~~~~~~~
If a line has a slope of #color(green)(2/3)# and passes through #(color(red)(-2),color(blue)(2))#
then it has a slope-point form of
#color(white)("XXX")y-color(blue)(2)=color(green)(2/3)(x-color(red)(""(-2)))#
Simplifying
#color(white)("XXX")y=color(green)(2/3)(x+2)+2#
#color(white)("XXX")3y=(2x+4) +6#
or (in standard form)
#color(white)("XXX")2x-3y+10=0#
~~~~~~~~~~~~~~~~~~~~~~
For verification/support, here are the graphs: