Question

How do you find all the critical points to graph `4x^2-9y^2=36` including vertices, foci and asymptotes?

Answer 1

Vertices `(+-3, 0)`
Focii `(+-sqrt13, 0)`
Asymptotes equations: `y=+-2/3x`

Explanation:

The equation `4x^2-9y^2=36` is a hyperbola

The standard form of the equation of a hyperbola is

`(x-h)^2/a^2-(y-k)^2/b^2=1`

For the given `4x^2-9y^2=36`

We divide both sides of the equation by `36`

`(4x^2-9y^2)/36=36/36`

`x^2/9-y^2/4=1`

it follows that

`(x-0)^2/(3^2)-(y-0)^2/(2^2)=1`

and by inspection and by comparing to the form above,

`(x-h)^2/a^2-(y-k)^2/b^2=1`

we have

`a=3` and `b=2` and
`c=sqrt(a^2+b^2)=sqrt(9+4)=sqrt13`
`c=sqrt13`

and center `(h, k)=(0, 0)`

Center `(h, k)=(0, 0)`
Vertices at `(h+a, k)= (+3, 0)`
and `(h-a, k)=(-3, 0)`

Focii at `(h+c, k)=(+sqrt13, 0)=(3.6, 0)`
and `(h-c, k)=(-sqrt13, 0)=(-3.6, 0)`

The equations of the asymptotes are given by the following formulas

`y=+-b/a(x-h)+k`

therefore,

`y=+-2/3(x-0)+0`

we have

`y=2/3x` and `y=-2/3x`

Kindly see the graphs of the hyperbola `4x^2-9y^2=36` colored red and asymptotes `y=2/3x` and `y=-2/3x` colored blue. You can also see the colored orange dots (Focii) and colored green dots (Vertices).

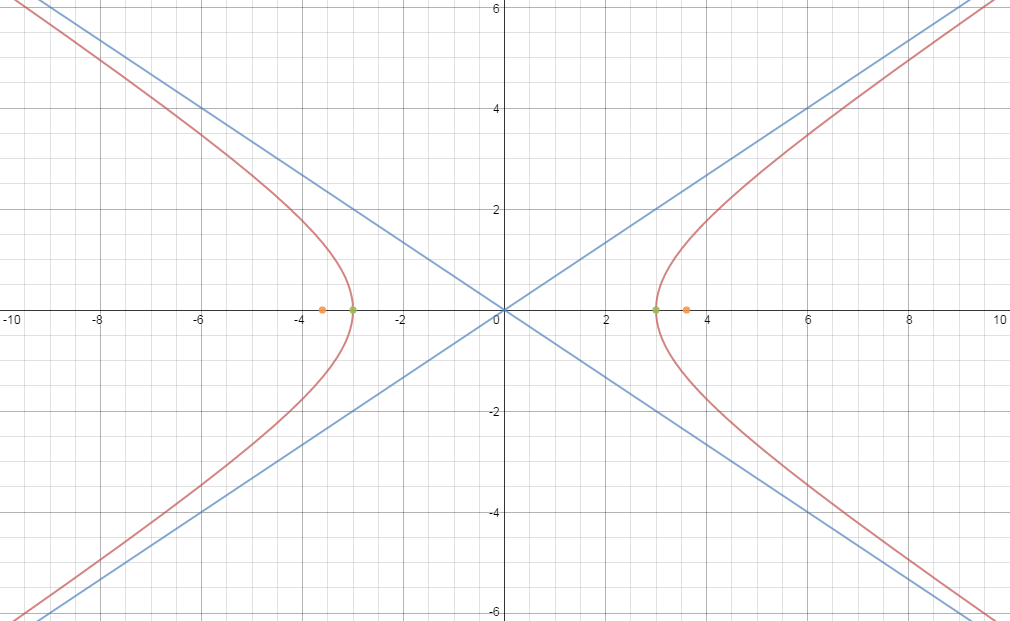
God bless... I hope the explanation is useful.