How do you find all the critical points to graph #9x^2 – y^2 – 36x + 4y + 23 = 0 # including vertices, foci and asymptotes?
2 Answers
A hyperbole
Explanation:
This conic can be represented formally with the structure
and is characterized as a hyperbole.
Forcing
we have the conditions
Solving for
characterizing
Also
The two lines
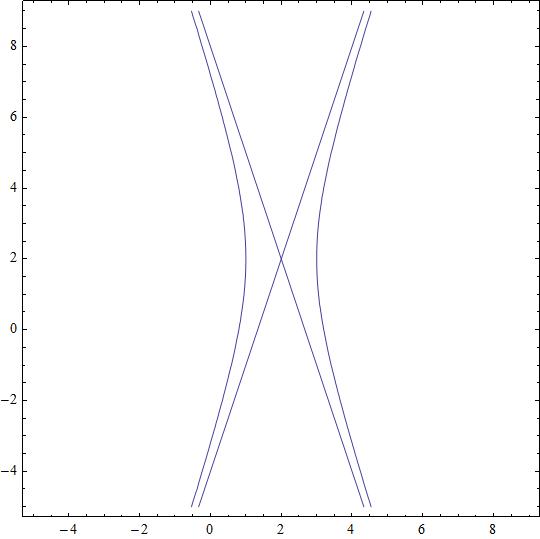
Explanation:
We complete the squares in the given eqn. to get the modified eqn.
Letting,
Comparing with,
Hence the Vertices, in
(0,+-b)=(0,+-3)#
In
(1,2)#.
The Eccentricity
Focii , in
Asymptotes in
So, in
Altogether,

