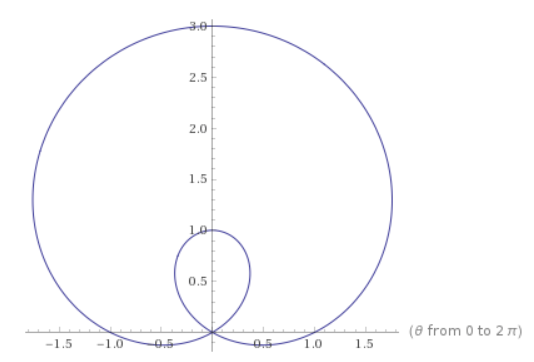
How do you find an equivalent equation in rectangular coordinates #r = 1 + 2 sin x#?
1 Answer
Mar 8, 2018
Explanation:
The relation between polar coordinates
Hence, we can write
as
or
The graph appears as follows (drawn using tool from Wolform):