How do you find Tan^-1(-1) without a calculator?
2 Answers
The answer is
Explanation:
Alright, archtan /
Knowing this we are solving for the inverse of tan -1. We are basically being asked the question what angle/radian does tan(-1) equal. Using the unit circle we can see that tan(1)= pi/4.
Since the "Odds and Evens Identity" states that tan(-x) = -tan(x). Tan(-1)= -pi/4.
Knowing that tan is negative in quadrants 2 and 4. the answer is in either of those two quadrants. BUT!!! since inverse of tan is restricted to quadrants 1 and 4 we are left with the only answer -pi/4.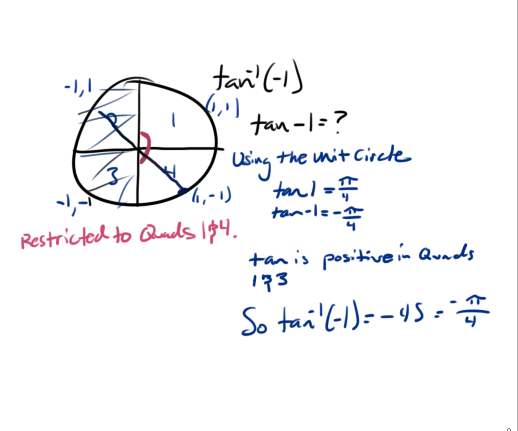
I am a college student taking Trig. please add any thing that could be wrong or added to benefit the answer. Hope this helped! :)
We reason
Explanation:
My answer's a bit more jaded than the other answer.
Trig students are only expected to know "exactly" the trig functions of two triangles, 30/60/90 and 45/45/90. It seems insane to have a whole field about just two triangles, but once you accept it trig becomes easier.
So you only need to know two triangles, but you need to know them in each quadrant, or at least be able to figure them out.
I really don't like the notation
We'll "solve" both
There's not a lot of solving involved. The expression
We have
So
The principal value for all these inverse functions are the continuous part which includes the first quadrant. Tangent blows up at
In radians

