Start by finding the intersection points.
#{(y = 2- 1/2x), (y = 2 - sqrt(x)):}#
#2 - sqrt(x) = 2 - 1/2x#
#1/2x = sqrt(x)#
#(1/2x)^2 = (sqrt(x))^2#
#1/4x^2 = x#
#1/4x^2 - x = 0#
#x(1/4x - 1) = 0#
#x = 0 and 4#
#:.y = 2 - sqrt(x)#
#y = 2 - sqrt(0) and y = 2 - sqrt(4)#
#y = 2 and 0#
The intersection points are hence #{0, 2}# and #{4, 0}#.
Now, we do a rudimentary sketch of the graphs on one grid (only if you don't have access to a graphing calculator, of course).
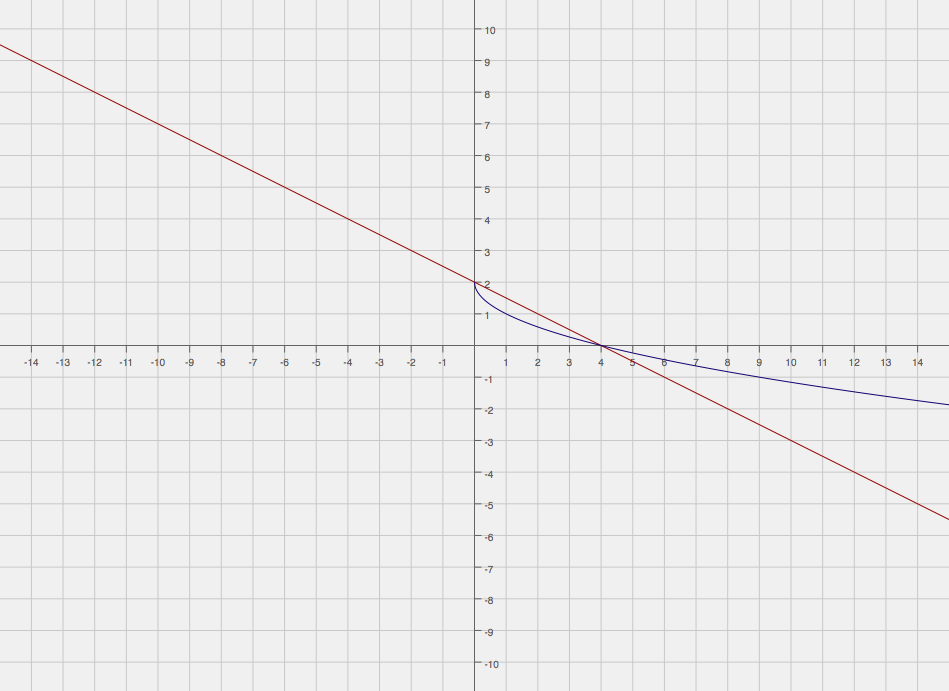
Our process here is to subtract the area of the lower graph (#y = 2-sqrt(x)#), from the area of the upper graph (#y = -1/2x + 2#). This will all be in the interval #0 ≤ x ≤ 4#.
We start by finding the area of the upper graph.
#int_0^4(-1/2x + 2)dx#
#=>(-1/4x^2 + 2x)|_0^4#
#=>-1/4(4^2) + 2(4) - (-1/4(0)^2 + 2(0))#
#=>-4 + 8 - 0#
#=> 4#
Now for the lower graph.
#int_0^4(2 - sqrt(x))dx#
#=>(2x - 2/3x^(3/2))|_0^4#
#=> 2(4) - 2/3(4)^(3/2) - (2(0) - 2/3(0)^(3/2))#
#=>8 - 16/3#
#=>8/3#
We now subtract the first area from the second:
#4 - 8/3 = 4/3#
Hence, the area of the region between #f(x) = 2 - 1/2x# and #g(x) = 2 - sqrt(x)# is #4/3" units"^2#.


