Question

How do you find the area between `f(x)=-x^2+4x+2, g(x)=x+2`?

Answer 1

We start by finding the intersection points of the two functions.

`{(y = -x^2 + 4x + 2), (y = x+ 2):}`

`x+ 2 = -x^2 + 4x + 2`

`x^2 - 3x = 0`

`x(x - 3) = 0`

`x = 0 and 3`

`y = 0 + 2 and y = 3 + 2`

`y = 2 and y= 5`

Hence, the intersection points are `(0, 2)` and `(3, 5)`.

We now do a rudimentary sketch of the two functions.

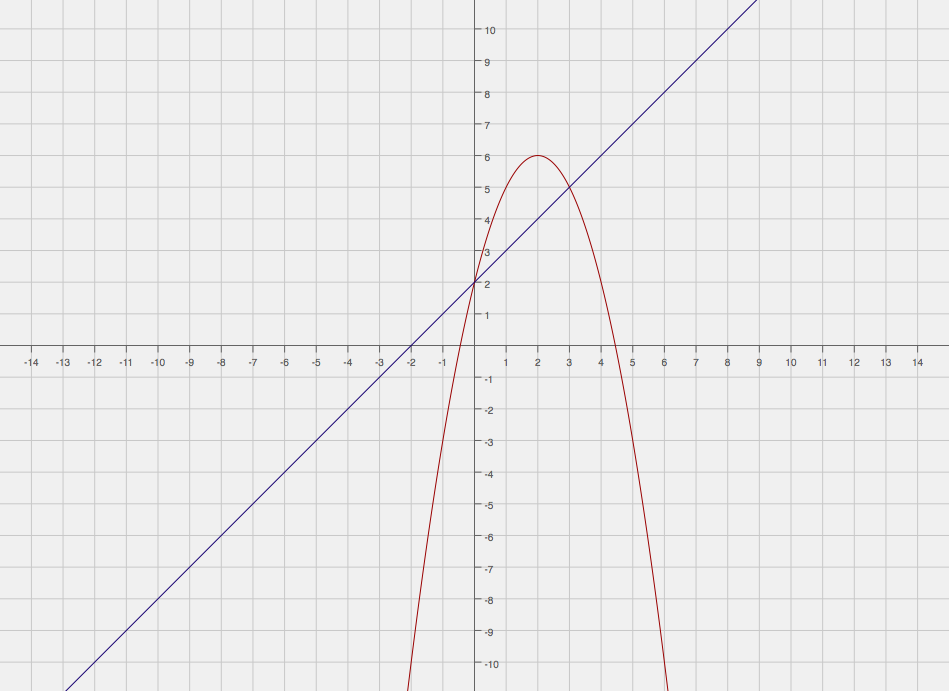
We always proceed in the following way: AREA BETWEEN CURVES = AREA OF CURVE ABOVE - AREA OF CURVE BELOW. We find this area using integration.

We will subtract the area under `y = x + 2` from `y = -x^2 + 4x + 2`.

`=>int_0^3(-x^2 + 4x + 2 - (x + 2))dx`

`=>int_0^3(-x^2 + 3x)`

`=>-1/3x^3 + 3/2x^2|_0^3`

`=>-1/3(3)^3 + 3/2(3)^2 - (-1/3(0)^3 + 3/2(0)^2)`

`=> -1/3(27) + 3/2(9)`

`=> -9 + 27/2`

`=> 9/2`

Hence, the area between the curves is `9/2" u"^2`.

Hopefully this helps!