How do you find the area between y=x, #y=1/x^2#, the xaxis and x=3?

Question

10553 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-13T11:04:36

#S=7/6#

First we note that:

#1/x^2 > 0# for any #x#

so the intercept between the curves and the #x#-axis must belong to the curve #y=x# and in fact occurs for #x=0#.

Then we analyze the inequality:

#x <= 1/x^2#

#x^3 <= 1#

#x<= 1#

This means that in the interval #[0,1]# the graph of #y=x# is below that of #y=1/x^2# while in the interval #[1,3]# the opposite occurs.

A picture can clarify that based on these considerations the area we seek is:

#S = int_0^1 xdx + int_1^3 (dx)/x^2#

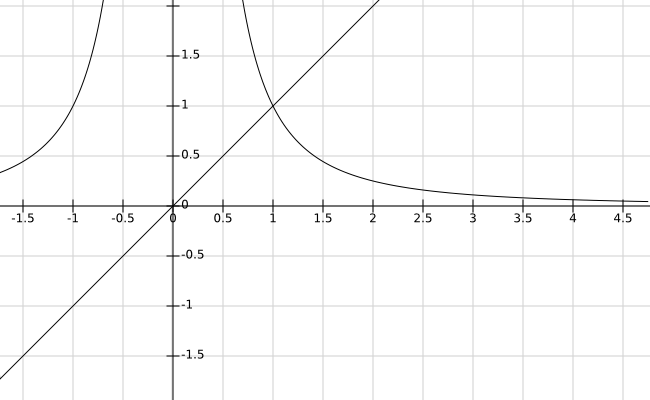
enter image source here

Performing the integral we obtain:

#S = int_0^1 xdx + int_1^3 (dx)/x^2 = [x^2/2]_0^1 -[1/x]_1^3 = 1/2-0-1/3 +1= 7/6 #