Start by finding the intersection points.
#x^2 + 1 = (x + 1)/x#
#x^3 + x = x + 1#
#x^3 = 1#
#x = 1#
This means that #y= 1^2 + 1 = 2#.
Now complete a rudimentary sketch of the graphs.
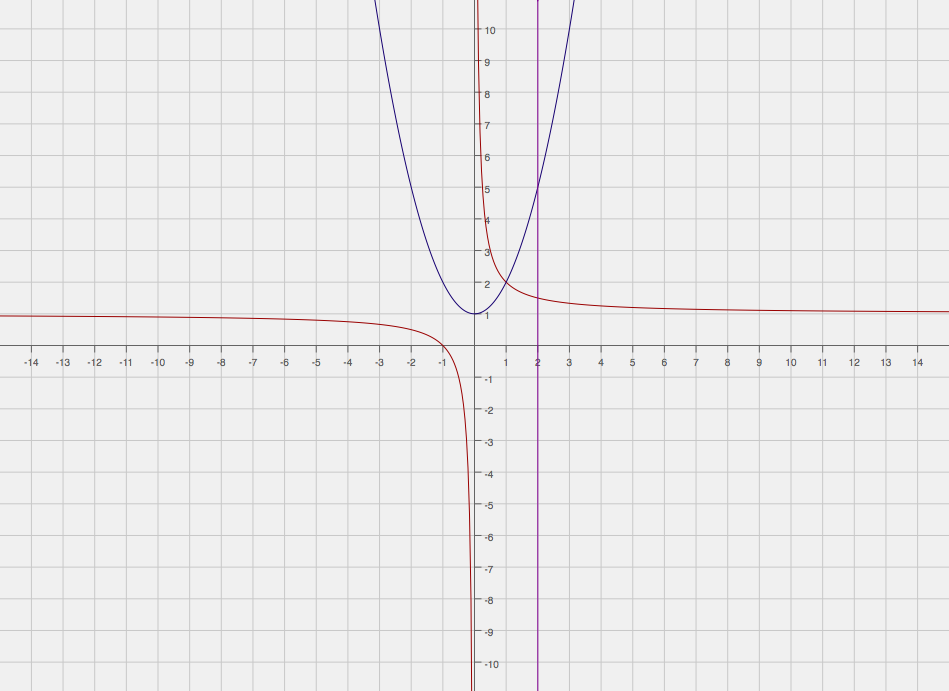
So we have bounds of integration of #[1, 2]# (this is why we found the intersection points), and we know the parabola lies above the rational function. The integral to evaluate will therefore be:
#int_1^2 x^2 + 1 - (x+ 1)/x dx#
#=int_1^2 (x^3 + x - x - 1)/xdx#
#=int_1^2 (x^3 - 1)/x dx#
#=int_1^2 x^2 - 1/xdx#
#=[1/3x^3 - ln|x|]_1^2#
Evaluate using #int_a^bF(x) = f(b) - f(a)#, where function #f(x)# is continuous on #[a, b]# and #f'(x) = F(x)#.
#=1/3(2)^3 - ln|2| - (1/3(1)^3 - ln|1|)#
#= 8/3 - ln2 - 1/3 + 0#
#= 7/3 - ln2#
Hopefully this helps!


