How do you find the area of a given hexagon is equal to the area of an equilateral triangle whose perimeter is 36 inches?
1 Answer
May 27, 2015
Warning: I suspect there is something wrong in the statement of this question; however....
If the perimeter of an equilateral triangle is 36 inches, each side is 12 inches and by the Pythagorean Theorem the height is
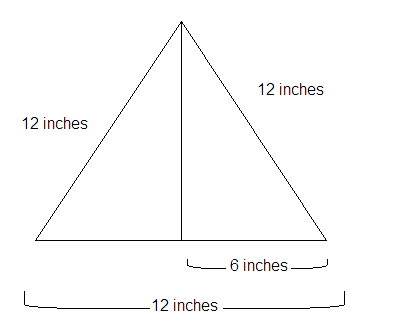
The area of the triangle is
