Question

How do you find the area of an isosceles triangle if the two equal sides are 10cm and the base is 12cm?

Answer 1

I found: `48"cm"^2`

Explanation:

Considering:

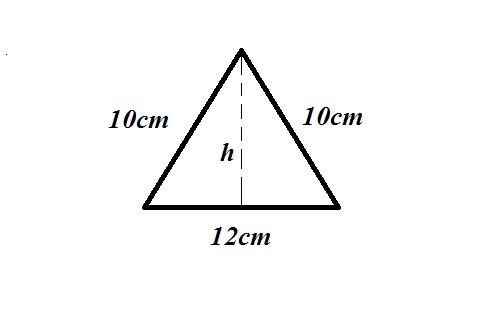
applying Pythagoras on half triangle you get:
`h^2+6^2=10^2`
`h=8cm`
So `Area=(basexxheight)/2=(12xx8)/2=48"cm"^2`

Answer 2

Area `= 48` sq. cm.
`color(white)("XXXX")` `color(white)("XXXX")`(Using Heron's formula)

Explanation:

As an alternate solution method:

Heron's Formula for the area of a triangle with sides `a, b, c`
`color(white)("XXXX")` `A = sqrt(s(s-a)(s-b)(s-c))`
`color(white)("XXXX")` `color(white)("XXXX")`where `s` is the semi-perimeter (i.e. `s= (a+b+c)/2`

In this case:
`color(white)("XXXX")` `s = 16`

`color(white)("XXXX")` `A = sqrt(16(6)(6)(4))`
`color(white)("XXXX")` `color(white)("XXXX")` `= sqrt(4^2*6^2*2^2)`
`color(white)("XXXX")` `color(white)("XXXX")` `=48`