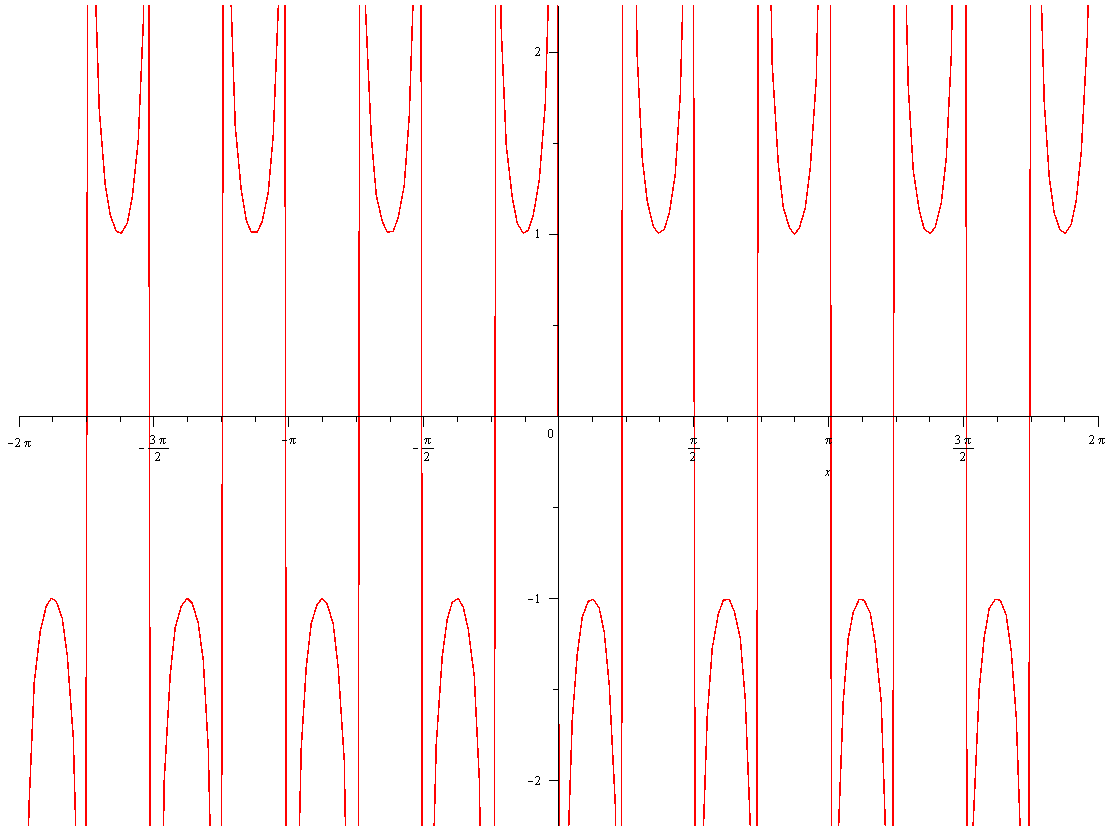
How do you find the asymptote for #y = csc (4x + pi)#?

Question

8314 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-12T19:23:02

See below.

Identity:

#color(red)bb(cscx=1/sinx)#

Vertical asymptotes occur where #1/sinx# is undefined.

i.e. where #sinx=0#

So:

#1/(sin(4x+pi)# will be undefined when. #sin(4x+pi)=0#

#:.#

#4x+pi=arcsin(sin(4x+pi)=arcsin(0)=0,pi,2pi# etc.

Using #2pi#

#4x+pi=2pi=>x=pi/4#

We can write all solutions as:

#npi/4#

Where n is an integer.

This is where all vertical asymptotes occur:

This is confirmed by the graph of #csc(4x+pi)#

enter image source here