Question

How do you find the axis of symmetry and vertex point of the function: `y= -1.5x^2+6x`?

Answer 1

Vertex: `(2, 6)`

Axis of symmetry: `x = 2`

Explanation:

`y = -1.5x^2 + 6x`

To find the `x`-coordinate of the vertex of a standard quadratic equation (y = ax^2 + bx + c), we use the formula `(-b)/(2a)`.

We know that `a = -1.5` and `b = 6`, so let's plug them into the formula:
`x = (-6)/(2(-1.5)) = -6/-3 = 2`

To find the `y`-coordinate of the vertex, just plug in the `x`-coordinate back into the original equation:
`y = -1.5x^2 + 6x`

`y = -1.5(2)^2 + 6(2)`

`y = -1.5(4) + 12`

`y = -6 + 12`

`y = 6`

Therefore, the vertex is at `(2, 6)`.

The axis of symmetry is the line of the `x`-coordinate of the vertex, so it's `x = 2`.

Here's a graph of this equation (desmos.com):

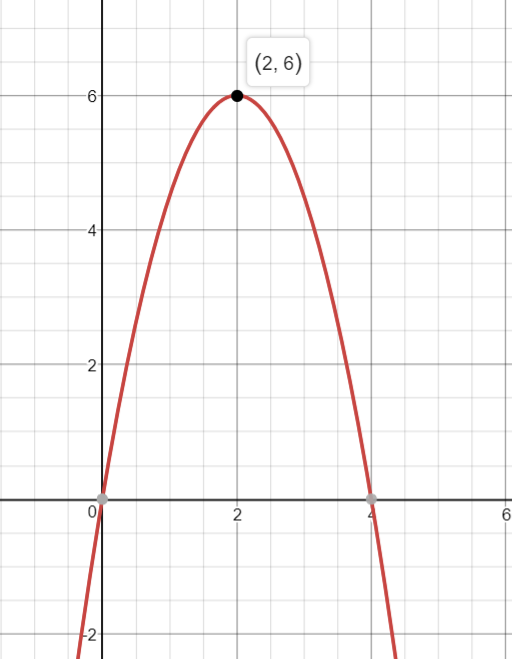
As you can see, the vertex is indeed at `(2, 6)`.

Hope this helps!