How do you find the center and radius of the circle #x^2+y^2-4x+8y-5=0 #?
1 Answer
Aug 25, 2016
Radius:
Center:
Explanation:
Do a double completion of square; the x's with the x's and the y's with the y's.
In the form
Hence, the centre is at
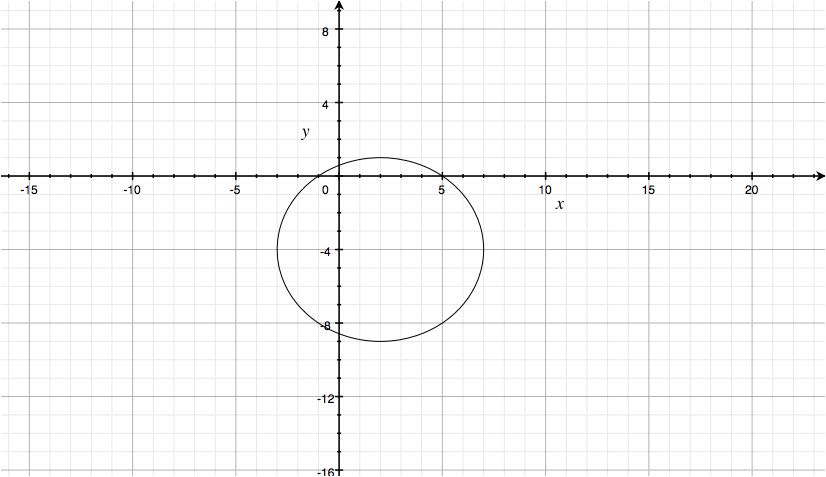
Hopefully this helps!

