How do you find the circumference of a circle circumscribed about a square with perimeter 40 in?

Question

7123 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-09T08:29:47

Perimeter of circle circumscribed about the square would be #44.4285# in .

As all the sides of a square are equal,

if its perimeter is #40#, each side is #40/4=10# in.

Now look at the following figure of a circle circumscribed about a square
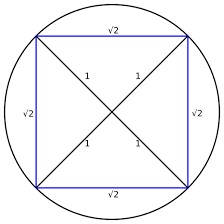
enter image source here

If the radius of a circle is #1# unit, the side of square by Pythagoras theorem is #sqrt(1^2+1^2)=sqrt(1+1)=sqrt2#

Now as side of square is #10#, radius of circle would be #10/sqrt2#,

and perimeter of a circle of radius #r# being #2pir#,

perimeter of circle circumscribed about the square would be

#2pixx10/sqrt2=10xxpixxsqrt2#

= #10xx3.1416xx1.4142=44.4285# in .