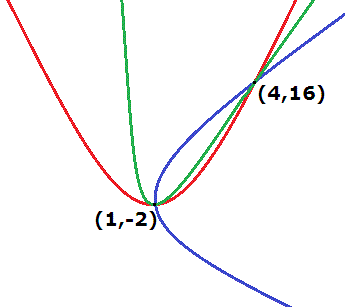Question

How do you find the equation of the parabola whose vertex is at (1,-2), and that passes through the point (4,16)?

Answer 1

`y=2x^2-4x`
`color(white)("XXXXXXXX")`(see note below)

Explanation:

Assuming the parabola is a function in standard position
with vertex at `(1,-2)` and another point at `(4,16)`

The general vertex form is
`color(white)("XXX")y=m(x-a)^2+bcolor(white)("XXX")` with vertex at `(a,b)`

For the given case;
`color(white)("XXX")y=m(x-1)^2-2`
at `(4,16)`
`color(white)("XXX")16 = m(3)^2-2 = 9m-2`
`rarrcolor(white)("XXX")m=2`

Therefore the equation is
`color(white)("XXX")y=2(x-1)^2-2`
`color(white)("XXXX")= 2x^2-4x`

Note: the general vertex form assumes the parabola is in standard position (e.g. with a vertical axis of symmetry). Infinitely many alternate solutions are possible if this is not the case.
Three such parabolas are shown below: