How do you find the exact value of #cos( 2 arctan (5/12) )#?
1 Answer
Jun 8, 2016
Explanation:
Use the cosine double angle formula:
#cos(2x)=2cos^2(x)-1#
Here, inside the cosine function, the angle
#cos(2arctan(5/12))=2cos^2(arctan(5/12))-1#
To find
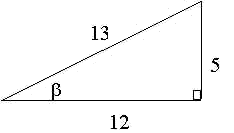
In this triangle,
So we see that
#2cos^2(arctan(5/12))-1=2(12/13)^2-1=288/169-1=119/169#

