Question

How do you find the exact value of `sec(arcsin(4/5))`?

Answer 1

`4/5`

Explanation:

Let `theta = arcsin(4/5)`. Then `sin(theta) = 4/5`.

Therefore:

`sin^2(theta) = 16/25`

`1 - sin^2(theta) = 1 - 16/25`

`1 - sin^2(theta) = 9/25`

`cos^2(theta) = 9/25`

`cos(theta) = +-3/5`

Note that `theta` must be between `-pi/2` and `pi/2` since this is the interval on which `arcsintheta` is defined. Also note that on the interval `-pi/2` to `pi/2`, `costheta` is always positive, since that interval covers all of the angles on the right half of the unit circle. Therefore:

`cos(theta) = 3/5`

`sec(theta) = 5/3`

`sec(arcsin(4/5)) = 5/3`

Final Answer

Answer 2

`5/3`

Explanation:

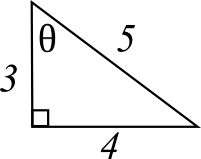
Alternatively, use the 3-4-5 right triangle as a shortcut to the problem.

We can see that `sin(theta) = "opposite"/"hypotenuse" = 4/5`.

Therefore, we can say that `theta = arcsin(4/5)`.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

We can also see that `cos(theta) = "adjacent"/"hypotenuse" = 3/5`.

Therefore, `sec(theta) = 1/cos(theta) = 5/3`

And, since we know `theta = arcsin(4/5)`, this means that:

`sec(arcsin(4/5)) = 5/3`

Final Answer