Question

How do you find the exact value of `sin^-1 0`?

Answer 1

`sin^-1(0)=npi` where n is an integer.

Explanation:

Let's start with the unit circle:

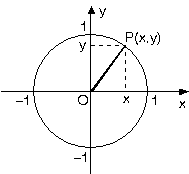
The sine ratio is the opposite divided by the hypotenuse:

`sin="opp"/"hyp"`

`sin^-1` asks us what the angle is that produces a ratio of a certain value. In this case, that ratio equals 0. For the ratio to be 0, the opposite side must equal 0 (if the hypotenuse were 0, the fraction would be undefined).

What angle produces an opposite side of 0?

Let's look again at the unit circle. A triangle is formed from Point O to Point P to the x and back to Point O. The side Px is the opposite side. Right now in the diagram, that distance is certainly bigger than 0. But if we move Point P down towards the x-axis (it moves along the unit circle) the opposite side gets closer and closer to 0 until, at the angle of 0 degrees, it is 0. And that is one angle that produces a sine ratio of 0.

The other angle is on the other side of the x-axis - again, with the Point P lying on the x-axis, the opposite side = 0 and therefore the sine ratio is 0.

We're almost done. The answer isn't limited to a range of values, so the exact value is:

`sin^-1(0)=npi` where n is an integer - this allows us to express not just 0 degrees but also `pi, 2pi, 3pi, -pi, -2pi` and so on.

We can see this in the graph of sin(x):

graph{sinx [-6.28, 6.28, -1.1, 1.1]}

Remember that `pi` = 3.14... and so we have `0pi` at the origin and `pi, 2pi, -pi, -2pi` on the graph. Each time the graph intersects the x-axis, that is where `sin^-1(0)`