Question

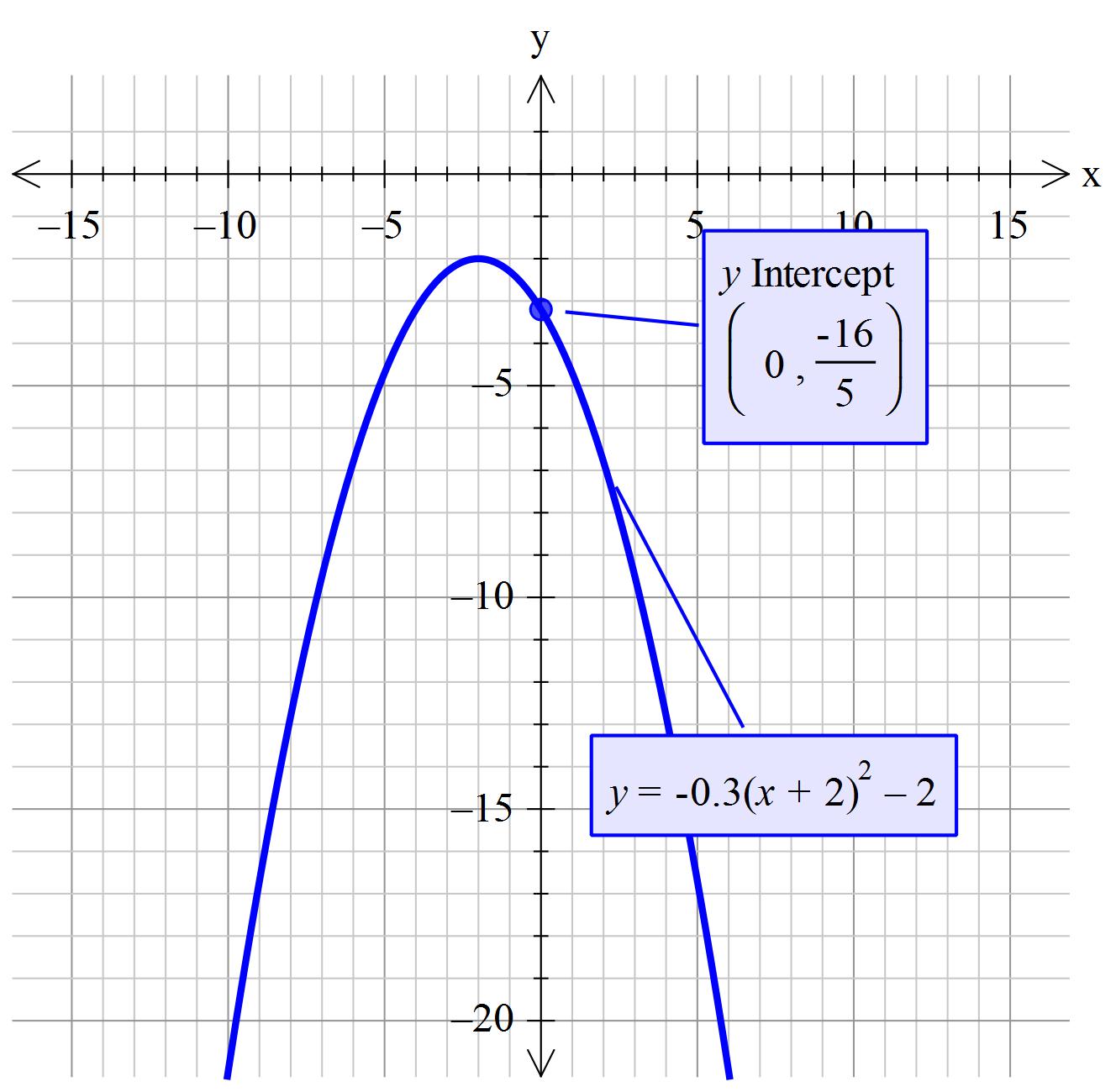
How do you find the intercept and vertex of `y= - .3(x+2)^2-2`?

Answer 1

No x intercepts
`y_("intercept")= -15/6`

Explanation:

Assumption: The question has -.3 which is assumed to mean - 0.3

The y intercept is at `x=0`

`=>y_("intercept")=-0.3(0+2)^2-2`

`y_("intercept")=(4xx0.3)-2 = (4xx3/10)-2`
`color(blue)(y_("intercept")= -(4xx3/10)-2 = -15/5)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

The x intercepts are at `y=0`

`=>0=-0.3(x+2)^2-2`

Add 2 to both sides

`0+2=-0.3(x+2)^2-2+2`

`2=-0.3(x+2)^2`

Divide both sides by `0.3`

`2/0.3 =-0.3/0.3(x+2)^2`

But `-0.3/0.3=-1`

`2/0.3=-(x+2)^2`

Multiply both sides by `-1`

`-2/0.3=+(x+2)^2`

Square root both sides

`x+2=sqrt( -2/0.3)`

As we are trying to take the square root of a negative number it means that the graph does not cross the x-axis. So there are no x intercepts